高考文科数学21题-高考文科数学题和理科数学题一样吗

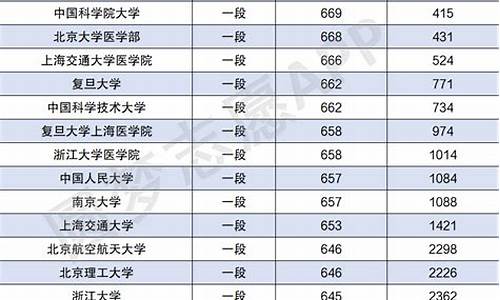
1.广东省普通高中文科数学试题

2.2013辽宁高考文科数学21题

3.函数求证题

4.2022年高考全国乙卷数学（经典版）（全）多种方法解析压轴题

广东省普通高中文科数学试题

一、 选择题（每小题5分，共60分）

（1）已知集合M={x|－3<x≤5},N={x|－5<x<5},则M∩N=

(A) {x|－5＜x＜5} (B) {x|－3＜x＜5}

(C) {x|－5＜x≤5} (D) {x|－3＜x≤5}

解析直接利用交集性质求解,或者画出数轴求解.

答案B

（2）已知复数 ，那么 =

（A） （B） （C） （D）

解析 ＝

答案D

（3）平面向量a与b的夹角为 ， ， 则

（A） (B) (C) 4 (D)12

解析由已知|a|＝2,|a＋2b|2＝a2＋4a?b＋4b2＝4＋4×2×1×cos60°＋4＝12

∴

答案B

（4）已知圆C与直线x－y=0 及x－y－4=0都相切，圆心在直线x+y=0上，则圆C的方程为

（A） (B)

(C) (D)

解析圆心在x＋y＝0上,排除C、D,再结合图象,或者验证A、B中圆心到两直线的距离等于半径2即可.

答案B

（5）从5名男医生、4名女医生中选3名医生组成一个医疗小分队，要求其中男、女医生都有，则不同的组队方案共有

（A）70种 （B） 80种 （C） 100种 （D）140种

解析直接法：一男两女,有C51C42＝5×6＝30种,两男一女,有C52C41＝10×4＝40种,共计70种

间接法：任意选取C93＝84种,其中都是男医生有C53＝10种,都是女医生有C41＝4种,于是符合条件的有84－10－4＝70种.

答案A

（6）设等比数列{ }的前n 项和为 ，若 =3 ，则 =

（A） 2 （B） （C） （D）3

解析设公比为q ,则 ＝1＋q3＝3 ? q3＝2

于是

答案B

（7）曲线y= 在点（1，－1）处的切线方程为

（A）y=x－2 (B) y=－3x+2 (C)y=2x－3 (D)y=－2x+1

解析y’＝ ,当x＝1时切线斜率为k＝－2

答案D

(8)已知函数 =Acos( )的图象如图所示， ，则 =

（A） (B) (C)－ (D)

解析由图象可得最小正周期为2π3

于是f(0)＝f(2π3),注意到2π3与π2关于7π12对称

所以f(2π3)＝－f(π2)＝

答案B

（9）已知偶函数 在区间 单调增加，则满足 ＜ 的x 取值范围是

（A）（ ， ） (B) 〔 ， ） (C)（ ， ） (D) 〔 ， ）

解析由于f(x)是偶函数,故f(x)＝f(|x|)

∴得f(|2x－1|)＜f( ),再根据f(x)的单调性

得|2x－1|＜ 解得 ＜x＜

答案A

（10）某店一个月的收入和支出总共记录了 N个数据 ， ，。。。 ，其中收入记为

正数，支出记为负数。该店用下边的程序框图计算月总收入S和月净盈利V，那么在图中空白的判断框和处理框中，应分别填入下列四个选项中的

（A）A>0,V=S－T

(B) A<0,V=S－T

(C) A>0, V=S+T

（D）A<0, V=S+T

解析月总收入为S,因此A＞0时归入S,判断框内填A＞0

支出T为负数,因此月盈利V＝S＋T

答案C

（11）正六棱锥P－ABCDEF中，G为PB的中点，则三棱锥D－GAC与三棱锥P－GAC体积之比为

（A）1：1 (B) 1：2 (C) 2：1 (D) 3：2

解析由于G是PB的中点,故P－GAC的体积等于B－GAC的体积

在底面正六边形ABCDER中

BH＝ABtan30°＝ AB

而BD＝ AB

故DH＝2BH

于是VD－GAC＝2VB－GAC＝2VP－GAC

答案C

（12）若 满足2x+ =5, 满足2x+2 (x－1)=5, + ＝

（A） (B)3 (C) (D)4

解析由题意 ①

②

所以 ,

即2

令2x1＝7－2t,代入上式得7－2t＝2log2(2t－2)＝2＋2log2(t－1)

∴5－2t＝2log2(t－1)与②式比较得t＝x2

于是2x1＝7－2x2

答案C

（13）某企业有3个分厂生产同一种电子产品，第一、二、三分厂的产量之比为1：2：1，用分层抽样方法（每个分厂的产品为一层）从3个分厂生产的电子产品中共取100件作使用寿命的测试，由所得的测试结果算得从第一、二、三分厂取出的产品的使用寿命的平均值分别为980h，1020h，1032h，则抽取的100件产品的使用寿命的平均值为 h.

解析 ＝1013

答案1013

（14）等差数列 的前 项和为 ，且 则

解析∵Sn＝na1＋ n(n－1)d

∴S5＝5a1＋10d,S3＝3a1＋3d

∴6S5－5S3＝30a1＋60d－(15a1＋15d)＝15a1＋45d＝15(a1＋3d)＝15a4

答案

（15）设某几何体的三视图如下（尺寸的长度单位为m）。

则该几何体的体积为

解析这是一个三棱锥,高为2,底面三角形一边为4,这边上的高为3,

体积等于 ×2×4×3＝4

答案4

（16）以知F是双曲线 的左焦点， 是双曲线右支上的动点，则 的最小值为 。

解析注意到P点在双曲线的两只之间,且双曲线右焦点为F’(4,0),

于是由双曲线性质|PF|－|PF’|＝2a＝4

而|PA|＋|PF’|≥|AF’|＝5

两式相加得|PF|＋|PA|≥9,当且仅当A、P、F’三点共线时等号成立.

答案9

（17）（本小题满分12分）

如图，A,B,C,D都在同一个与水平面垂直的平面内，B，D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为 ， ，于水面C处测得B点和D点的仰角均为 ，AC=0.1km。试探究图中B，D间距离与另外哪两点间距离相等，然后求B，D的距离（计算结果精确到0.01km， 1.414， 2.449）

(17)解:

在△ABC中，∠DAC=30°, ∠ADC=60°－∠DAC=30,

所以CD=AC=0.1 又∠BCD=180°－60°－60°=60°，

故CB是△CAD底边AD的中垂线，所以BD=BA， ……5分

在△ABC中，

即AB=

因此，BD=

故B，D的距离约为0.33km。 ……12分

（18）（本小题满分12分）

如图，已知两个正方行ABCD 和DCEF不在同一平面内，M，N分别为AB，DF的中点。

（I）若平面ABCD ⊥平面DCEF，求直线MN与平面DCEF所成角的正值弦；

（II）用反证法证明：直线ME 与 BN 是两条异面直线。

（18）（I）解法一：

取CD的中点G，连接MG，NG。

设正方形ABCD，DCEF的边长为2，

则MG⊥CD，MG=2，NG= .

因为平面ABCD⊥平面DCED，

所以MG⊥平面DCEF，

可得∠MNG是MN与平面DCEF所成的角。因为MN= ，所以sin∠MNG= 为MN与平面DCEF所成角的正弦值 ……6分

解法二：

设正方形ABCD，DCEF的边长为2，以D为坐标原点，分别以射线DC，DF，DA为x,y,z轴正半轴建立空间直角坐标系如图.

则M（1,0,2）,N(0,1,0),可得 =(－1,1,2).

又 =（0，0，2）为平面DCEF的法向量，

可得

所以MN与平面DCEF所成角的正弦值为

cos ? ……6分

(Ⅱ)假设直线ME与BN共面， ……8分

则AB 平面MBEN，且平面MBEN与平面DCEF交于EN

由已知，两正方形不共面，故AB 平面DCEF。

又AB//CD，所以AB//平面DCEF。面EN为平面MBEN与平面DCEF的交线，

所以AB//EN。

又AB//CD//EF，

所以EN//EF，这与EN∩EF=E矛盾，故假设不成立。

所以ME与BN不共面，它们是异面直线. ……12分

（19）（本小题满分12分）

某人向一目射击4次，每次击中目标的概率为。该目标分为3个不同的部分，第一、二、三部分面积之比为1：3：6。击中目标时，击中任何一部分的概率与其面积成正比。

（Ⅰ）设X表示目标被击中的次数，求X的分布列；

（Ⅱ）若目标被击中2次，A表示事件“第一部分至少被击中1次或第二部分被击中2次”，求P（A）

（19）解：

（Ⅰ）依题意X的分列为

0 1 2 3 4

P

………………6分

（Ⅱ）设A1表示事件“第一次击中目标时，击中第i部分”，i=1，2.

B1表示事件“第二次击中目标时，击中第i部分”，i=1，2.

依题意知P（A1）=P(B1)=0.1，P（A2）=P(B2)=0.3，

,

所求的概率为

………12分

（20）（本小题满分12分）

已知，椭圆C过点A ，两个焦点为（－1，0），（1，0）。

（1） 求椭圆C的方程；

（2） E,F是椭圆C上的两个动点，如果直线AE的斜率与AF的斜率互为相反数，证明直线EF的斜率为定值，并求出这个定值。

（20）解：

（Ⅰ）由题意，c=1,可设椭圆方程为 ，解得 ， （舍去）

所以椭圆方程为 。 ……………4分

（Ⅱ）设直线AE方程为： ，代入 得

设 , ,因为点 在椭圆上，所以

………8分

又直线AF的斜率与AE的斜率互为相反数，在上式中以—K代K，可得

所以直线EF的斜率

即直线EF的斜率为定值，其值为 。 ……12分

（21）（本小题满分12分）

已知函数f(x)= x －ax+(a－1) ， 。

（1）讨论函数 的单调性；

（2）证明：若 ，则对任意x ，x ，x x ，有 。

(21)解：(1) 的定义域为 。

2分

（i）若 即 ,则

故 在 单调增加。

(ii)若 ,而 ,故 ,则当 时， ;

当 及 时，

故 在 单调减少，在 单调增加。

(iii)若 ,即 ,同理可得 在 单调减少，在 单调增加.

(II)考虑函数

则

由于1<a<5,故 ，即g(x)在(4, +∞)单调增加，从而当 时有 ，即 ，故 ，当 时，有 ?12分

请考生在第（22）、（23）、（24）三题中任选一题做答，如果多做，则按所做的第一题记分。做答时用2B铅笔在答题卡上把所选题目的题号涂黑。

（22）（本小题满分10分）选修4－1：几何证明讲

已知 ABC 中，AB=AC, D是 ABC外接圆劣弧 上的点（不与点A,C重合），延长BD至E。

（1） 求证：AD的延长线平分 CDE；

（2） 若 BAC=30， ABC中BC边上的高为2+ ，求 ABC外接圆的面积。

（22）解：

（Ⅰ）如图，设F为AD延长线上一点

∵A，B，C，D四点共圆，

∴∠CDF=∠ABC

又AB=AC ∴∠ABC=∠ACB,

且∠ADB=∠ACB, ∴∠ADB=∠CDF,

对顶角∠EDF=∠ADB, 故∠EDF=∠CDF,

即AD的延长线平分∠CDE.

（Ⅱ）设O为外接圆圆心，连接AO交BC于H,则AH⊥BC.

连接OC,A由题意∠OAC=∠OCA=150, ∠ACB=750,

∴∠OCH=600.

设圆半径为r,则r+ r=2+ ,a得r=2,外接圆的面积为4 。

（23）（本小题满分10分）选修4－4 ：坐标系与参数方程在直角坐标系xOy中，以O为极点，x正半轴为极轴建立极坐标系，曲线C的极坐标方程为 cos（ ）=1，M,N分别为C与x轴，y轴的交点。

（1）写出C的直角坐标方程，并求M,N的极坐标；

（2）设MN的中点为P，求直线OP的极坐标方程。

（23）解：

（Ⅰ）由

从而C的直角坐标方程为

（Ⅱ）M点的直角坐标为（2，0）

N点的直角坐标为

所以P点的直角坐标为

所以直线OP的极坐标方程为

（24）（本小题满分10分）选修4－5：不等式选讲

设函数 。

（1）若 解不等式 ；

（2）如果 , ,求 的取值范围。

（24）解：

（Ⅰ）当a=－1时，f(x)=｜x－1｜+｜x+1｜.

由f(x)≥3得

｜x－1｜+｜x+1|≥3

x≤－1时，不等式化为

1－x－1－x≥3 即－2x≥3

不等式组 的解集为[ ，+∞),

综上得， 的解集为 ……5分

（Ⅱ）若 ，不满足题设条件

若 ， 的最小值为

若 ， 的最小值为

所以 的充要条件是| -1|≥2，从而 的取值范围为

2013辽宁高考文科数学21题

ax-4+2(x+2)cosx+x^2+1/2*x^3=(a+2)x+x^2+1/2*x^3-4(x+2)(sinx/2)^2

<=(a+2)x+x^2+1/2*x^3-4(x+2)(二分之根号二*1/2*x)^2=(a+2)x<=0

所以a<=-2

而0<=x<=1时，0<=sinx/2<=sin1/2<=四分之根号二

如果题目x的范围是0<=x<=四分之派，则证明可省略

函数求证题

这是2007年高考天津数学(文科)试题的21题

答案如下：

(21)(Ⅰ)解：当a=1时，f(x)=-x(x-1)2=-x3+2x2-x，得f(2)=-2，且f′(x)=-3x2+4x-1，f′(2)=-5.

所以，曲线y=-x(x-1)2在点(2,-2)处的切线方程是y+2=-5(x-2)，整理得5x+y-8=0.

(Ⅱ)解：f(x)=-x(x-a)2=-x3+2ax2-a2x，

f′(x)=-3x2+4ax-a2=-(3x-a)(x-a).

令f′(x)=0，解得或x=a.

由于a≠0，以下分两种情况讨论.

(1)若a＞0，当x变化时，f′(x)的正负如下表：

x (-∞,a/3) a/3 (a/3,a) a (a,+∞)

f′(x) - 0 + 0 -

因此，函数f(x)在处取得极小值，且；函数f(x)在x=a处取得极大值f(a)，且f(a)=0.

(2)若a＜0，当x变化时，f′(x)的正负如下表：

x (-∞,a) a (a/3a, ) a/3 (a/3,+∞)

f'(x) - 0 + 0 -

因此，函数f(x)在x=a处取得极小值f(a)，且f(a)=0；函数f(x)x=a/3在处取得极大值f(a/3)=-4/27 a^3

(Ⅲ)证明：由a＞3，得a/3＞1，当k∈[-1,0]时，k-cosx≤1，k2-cos2x≤1.

由(Ⅱ)知，f(x)在(-∞,1]上是减函数，要使f(k-cosx)≥f(k2-cos2x)，x∈R，只要k-cosx≤k2-cos2x(x∈R)，即

cos2x-cosx≤k2-k(x∈R).①

设g(x)cos^2x-cosx=(cosx-1/2)^2-1/4，则函数g(x)在R上的最大值为2.

要使①式恒成立，必须k^2-k≥2，即k≥2或k≤-1.

所以，在区间[-1,0]上存在k=-1，使得f(k-cosx)≥f(k2-cos2x)对任意的x∈R恒成立.

可以参考（- - ！网址有点长~~ 这是题目及答案~）

2022年高考全国乙卷数学（经典版）（全）多种方法解析压轴题

2022年高考全国乙卷数学（经典版）（全）全方位、不同视角、多种方法解析压轴题

单选压轴题：两个角度解析2022年高考全国乙卷理科数学试题第9题

正弦定理与离心率：全方位解析2022年高考全国乙卷理科数学试题第11题

选择题压轴题：从两个不同方向解析2022年高考全国乙卷理科数学试题第12题

单选压轴题：两个角度解析2022年高考全国乙卷文科数学试题第12题

半分离，全分离，常规解法：三种方法解析2022年高考全国乙卷理科数学试题第16题

常规推导+分离参数：多方法解析2022年高考全国乙卷文科数学试题第20题第（2）问

2022年高考运算最复杂试题最简单解法（第三个方法）以2022年高考全国乙卷理科数学第20题为例再探圆锥曲线极点与极线性质定理

2022年高考运算最复杂试题最简单解法（第三个方法）以2022年高考全国乙卷文科数学第21题为例再探圆锥曲线极点与极线性质定理

函数零点个数问题：多方法解析2022年高考全国乙卷理科数学试题第21题