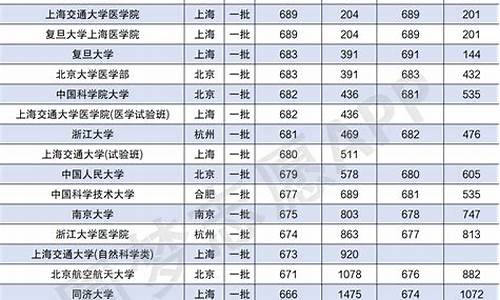
高考数学难题分布,高考数学难题

1.数学高考难题请求帮助？

2.数学高考难题请求帮助3

3.高考数学难题请求帮助2

4.数学高考难题请求帮助

5.第八题，高考数学难题，请哪位帮忙做一下，在线等。谢谢

6.2022年上海成人高考高升本《数学》难题讲解(二)？

7.数学高考难题请求帮助1

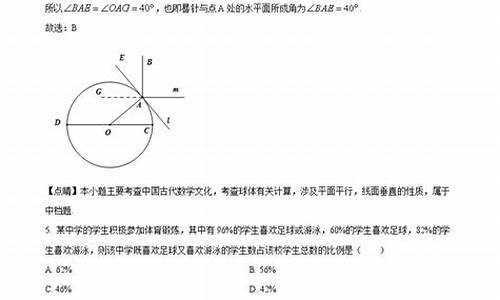
设C点坐标为（X,Y）

OC相量＝α?OA相量＋β?OB相量

这个式子可以确定两个关系

一个是α，β和X的关系

一个是α，β和y的关系

用α＋β＝1关系β=1-α消去上两个式子中的α

在用消去β

就可以得到XY的关系

数学高考难题请求帮助？

所有情况共有C(40,2)*C(38,2)=548340种

(先从40张牌中选出2张给其中一家,再从38张牌中选出2张给下一家)

1.对子相等的情况:

有C(10,1)*C(4,2)=60种.

(先从1到10选出一个数,再从这个数的4张牌中选出2个给其中一家,那另一家则别无选择)

2.点数相等的情况:

分牌面一样和不一样的,

(1)如果一样的,比如{2,6}对{2,6}

这样的情况共有:C(10,2)*A(4,2)*A(4,2)=5480种.

(既然不是对子,先从1到10中选出两个数,再对每一个数字的4张牌中有次序的选出各两张分给两家)

(2)如果点数一样,牌面不一样

都是0点:{1,9},{2,8},{3,7},{4,6}共4个类型

都是1点:{1,10},{2,9},{3,8},{4,7},{5,6}共5个类型

都是2点:{2,10},{3,9},{4,8},{5,7}共4个类型

都是3点:{1,2},{3,10},{4,9},{5,8},{6,7}共5个类型

都是4点:{1,3},{4,10},{5,9},{6,8}共4个类型

都是5点:{1,4},{2,3},{5,10},{6,9},{7,8}共5个类型

都是6点:{1,5},{2,4},{6,10},{7,9}共4个类型

都是7点:{1,6},{2,5},{3,4},{7,10},{8,9}共5个类型

都是8点:{1,7},{2,6},{3,5},{8,10}共4个类型

都是9点:{1,8},{2,7},{3,6},{4,5},{9,10}共5个类型

偶数点数共有C(5,1)*A(4,2)*C(4,1)*C(4,1)*C(4,1)*C(4,1)=15360种

(先从5个偶数点数中选出一个,再从4个类型中有次序的选出两个类型分给两个人,然后两个人从本类型的两个数字的4张牌中各选出一个,要选4次,每次都是4选1)

奇数点数共有C(5,1)*A(5,2)*C(4,1)*C(4,1)*C(4,1)*C(4,1)=25600种

(先从5个奇数点数中选出一个,再从5个类型中有次序的选出两个类型分给两个人,然后两个人从本类型的两个数字的4张牌中各选出一个,要选4次,每次都是4选1)

总之,庄家和闲家牌大小相等的,包括对子和点数,

一起有60+5480+15360+25600=46500种

其余共有548340-46500=501840

这些情况根据对称性原理.应该两家大小机会平等.

所以各人有250920种情况是要赢的,考虑大小相等庄家赢

所以庄赢的种类为250920+46500=297420

概率为297420/548340=4957/9139.

我只计算了赌一次庄赢的概率.

不考虑翻倍和赌注大小.如果考虑的话算出来的就是此赌法长期大量下去对哪家有利.那要算期望,也不难算.

数学高考难题请求帮助3

由f（x）=cos〔ω（x＋θ）〕是奇函数,f（-x）=-f（x）

则cos〔ω（-x＋θ）〕=-cos〔ω（x＋θ）〕

即cos〔ω（-x＋θ）〕=cos〔-ω（x＋θ）〕

于是ω（-x＋θ）=-ω（x＋θ）+2kπ 或 ω（-x＋θ）=2π-(-ω（x＋θ）)+2kπ

解之得θ=kπ/ω 或者 x=-(2k+1)π/(2ω)(舍)

(S中的元素由所有的θ组成)

θ的周期是T=π/ω

由"若对每个实数a，S∩（a，a+1）的元素不超过2个"知2T>=1(1=a+1-a),即ω≤2π;

由"有a使S∩（a，a+1）含2个元素，求ω的取值范围"知T<1,即ω>π.

综上,π＜ω≤2π

(后面求ω取值范围时画个数轴就很容易理解了)

高考数学难题请求帮助2

解答：用图象法。

首先，在方程y＝√(1－x^2)中，1－x^2≥0，

所以：x^2≤1，-1≤x≤1.

另外，显然y≥0。并且这个方程可以变为：

x^2+y^2=1。

所以，曲线C的图象是单位圆的上半圆.

（这里楼主要开始图画了）

而直线L：y＝x＋b的斜率是1，即倾斜角是45°，

先将直线放在圆的左边与圆相离的地方，

然后从左至右移动直线，发现：

(1)当直线与圆相切时，直线与圆只有一个交点；

(2)继续平移直线，直线与圆就有2个交点了；

(3)当直线过点(-1,0)和(0,1)时,直线与圆还有2个交点；

(4)继续向右平移直线，直线与圆只有1个交点了。

所以，所求的b的取值范围介于以上的(1)(3)两种情况之间。

情况(1)：直线与圆相切，由方程组

y＝x+b，

x^2+y^2=1

消去y得：2x^2+2bx+b^2-1＝0，

根据判别式Δ＝4b^2-8(b^2-1)=0,

得：b＝√2。（这里负数根舍）

情况(3):显然，b＝1。

综上，所求的范围是：1≤b＜√2。

数学高考难题请求帮助

四边形PAOB的面积S=1/2（PA+PB)R 因为R=2所以S=PA+PB 根据均值不等式，当PA=PB时，S最小，PO即为0点到直线的距离，根据勾股定理可解得PA=PB=4 所以S=8

第八题，高考数学难题，请哪位帮忙做一下，在线等。谢谢

直线x－2y＋4＝0与直线2x－y－1＝0的交点解得：(2,3)；

设直线的点斜式方程：y-3=k(x-2),即kx-y+(3-2k)=0，因为直线与A、B距离相等，利用点到直线公式：

|k*0-4+(3-2k)|=|4k+(3-2k)|，解这个含绝对值的方程，得：k=-1，

所以所求直线方程：-x-y+1=0,即x+y-1=0；

你的标准答案有误。

2022年上海成人高考高升本《数学》难题讲解(二)？

假设B1D与平面A1BC1的交点为O，

易证B1D与平面A1BC1垂直，所以，PO与直线B1D垂直，

B1D=AB*√3=3*√3

(1/3)*B1O*S△A1BC1=(1/3)*A1B1*(1/2)*BB1*B1C1

B1O=√3

DO=DB1-B1O=2√3

PD=√(DO*DO+PO*PO)=√(12+OP*OP)

PB1=√(3+PO*PO)

PD+PB1=2+√13=[√(12+OP*OP)]+√(3+PO*PO)

PO*PO=1

P点在平面A1BC1内，以O为圆心，半径为1的圆上，

PB1=2

AD1与BC1平行，过点B1作BC1的平行线，交CB的延长线于点E，连接PE，

角PB1E即为直线B1P与直线AD1的夹角的平面角，

B1E=BC1=3√2

cos∠PB1E=(PB1^2+B1E^2-PE^2)/(2*PB1*B1E)=(20-PE^2)/(12√2)

显然当线段PE最小时，cos∠PB1E最大，

当线段PE最大时，cos∠PB1E最小，

数学高考难题请求帮助1

成考快速报名和免费咨询： 猎考网整理了2022年上海成人高考高升本《数学》难题讲解(二)，对专升本数学考试难点进行梳理。希望文章的考试难点可以帮助到大家。一起来看看吧!　　2022年上海成人高考高升本《数学》难题讲解(二)

一、函数、极限和连续

(一)函数

1.知识范围

(1)函数的概念

函数的定义 函数的表示法 分段函数 隐函数

(2)函数的性质

单调性 奇偶性 有界性 周期性

(3)反函数

反函数的定义 反函数的图像

二、平面与直线

1.知识范围

(1)常见的平面方程

点法式方程 一般式方程

(2)两平面的位置关系(平行、垂直和斜交)

(3)点到平面的距离

(4)空间直线方程

标准式方程(又称对称式方程或点向式方程)一般式方程参数式方程

(5)两直线的位置关系(平行、垂直)

(6)直线与平面的位置关系(平行、垂直和直线在平面上)

2.要求

(1)会求平面的点法式方程、一般式方程。会判定两平面的垂直、平行。会求两平面间的夹角。

(2)会求点到平面的距离。

(3)了解直线的一般式方程，会求直线的标准式方程、参数式方程。会判定两直线平行、垂直。

(4)会判定直线与平面间的关系(垂直、平行、直线在平面上)。

成考服务

1、想了解备考相关问题，点击在线咨询了解更多!

2、点击考生交流群和其他考生一起打卡备考!

成考有疑问、不知道如何总结成考考点内容、不清楚成考报名当地政策，点击底部咨询官网，免费领取复习资料： AB(1,X) BC(X+2tanθ－1,y-x+1)

对应系数成比例 解得y=x^2+2xtanθ－1

(2) 配方 y＝(x+tanθ)^2-(tanθ)^2-1

对称轴－tanθ <=-1 或>=根号3

解得θ属于（－π／2，－π／3∪π／4，π／2）

(3) 当π/4≤θ≤π/3 对称轴在－1左

x取－1时 有最小值 代入得g（θ）＝－2tanθ

当－π/3≤θ≤π/4 对称轴在（－1，根号3）内 x取－tanθ

有最小值 此时g（θ）＝－tanθ^2 -1