2017福建数学高考答案_2017福建数学会考

1.2017年高考数学必考等差数列公式

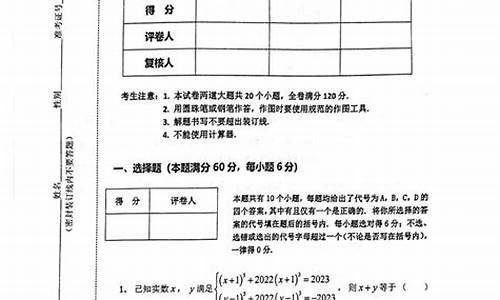
2.2017年全国一卷数学高考题，如图，答案最后为什么写m＞负一？

f'(x)=2ax+(2-a)-1/x

=(2ax^2+(2-a)x-1)/x

=(2x-1)(ax+1)/x

a>1

令f'(x)>=0

x<=-1/a或x>=1/2

定义域是x>0

∴x>=1/2

增区间是[1/2,+∞),减区间是(0,1/2]

当1/a>=1/2时

f(x)在区间[1/a,1]内的最大值

=f(1)

=a+2-a-0

=2不是ln3

∴1/a<1/2

a>2

f(x)在区间[1/a,1]内的最大值

=f(1/a)

=a*1/a^2+(2-a)/a-ln(1/a)

=1/a+2/a-1+lna

=3/a-1+lna

=ln3

∴a=3符合a>2

综上a=3

如果您认可我的回答，请点击“为满意答案”,祝学习进步！

2017年高考数学必考等差数列公式

二次方程求根公式的得出，两条直线位置关系的确定，无穷小量的得出，等等。数学运算、数学推理、数学证明、数学理论的正确性等，不能像自然科学那样借助于可重复的实验来检验，而只能借助于严密的逻辑方法来实现这时，班里的大姐——淑婷站在台阶上准备吹出巨大型泡泡。她用吸管飞速地转了转泡泡水，不知转了几圈后她才罢休。接下来淑婷又盖上盖子，用力晃了晃泡泡瓶，她那几道工序看的我们大家真是眼花缭乱，不知哪个同学在台下喊了一声:“你要叫我们我们等到猴年马月呀。”淑婷不慌不忙地回答了一声：“眼睛睁大了，见证奇迹的时刻到了。”刹那间，巨大的泡泡慢悠悠地飘在半空中，大家都“哇”了一声。我赶忙再吹出几个小泡泡围绕在它身边，瞧，几个小泡泡和一个大泡泡在跳着华尔兹呢！同学们也再纷纷吹出几个小泡泡，天空中顿时飘满了五颜六色的泡泡，它们或许在与白云为伴，日月同升……“叮铃铃”这突如其来的下课铃声把泡泡吓到躲起来了，突然变得无影无踪。我们赶紧再吹出几十个泡泡，这下更多了。全校同学们都陷入了泡泡乡，校园一下子变成了泡泡的故居。

2017年全国一卷数学高考题，如图，答案最后为什么写m＞负一？

　等差数列是常见数列的一种，如果一个数列从第二项起，每一项与它的前一项的差等于同一个常数，这个数列就叫做等差数列。以下是我为您整理的关于2017年高考数学必考等差数列公式的相关资料，希望对您有所帮助。

　高中数学知识点：等差数列公式

　等差数列公式an=a1+(n-1)d

　a1为首项，an为第n项的通项公式，d为公差

　前n项和公式为：Sn=na1+n(n-1)d/2

　Sn=(a1+an)n/2

　若m+n=p+q则：存在am+an=ap+aq

　若m+n=2p则：am+an=2ap

　以上n.m.p.q均为正整数

　解析：第n项的值an=首项+(项数-1)?公差

　前n项的和Sn=首项?n+项数(项数-1)公差/2

　公差d=(an-a1)?(n-1)

　项数=(末项-首项)?公差+1

　数列为奇数项时，前n项的和=中间项?项数

　数列为偶数项，求首尾项相加，用它的和除以2

　等差中项公式2an+1=an+an+2其中{an}是等差数列

　通项公式：公差?项数+首项-公差

　高中数学知识点：等差数列求和公式

　若一个等差数列的首项为a1，末项为an那么该等差数列和表达式为：

　S=(a1+an)n?2

　即(首项+末项)?项数?2

　前n项和公式

　注意：n是正整数(相当于n个等差中项之和)

　等差数列前N项求和，实际就是梯形公式的妙用：

　上底为：a1首项，下底为a1+(n-1)d，高为n。

　即[a1+a1+(n-1)d]* n/2={a1n+n(n-1)d}/2。

　高中数学知识点：推理过程

　设首项为 , 末项为 , 项数为 , 公差为 , 前 项和为 , 则有:

　当d?0时，Sn是n的二次函数，(n，Sn)是二次函数 的图象上一群孤立的点。利用其几何意义可求前n项和Sn的最值。

　注意：公式一二三事实上是等价的，在公式一中不必要求公差等于一。

　求和推导

　证明：由题意得：

　Sn=a1+a2+a3+。。。+an①

　Sn=an+a(n-1)+a(n-2)+。。。+a1②

　①+②得：

　2Sn=[a1+an]+[a2+a(n-1)]+[a3+a(n-2)]+...+[a1+an](当n为偶数时)

　Sn={[a1+an]+[a2+a(n-1)]+[a3+a(n-2)]+...+[a1+an]}/2

　Sn=n(A1+An)/2 (a1，an，可以用a1+(n-1)d这种形式表示可以发现括号里面的数都是一个定值，即(A1+An)

　基本公式

　公式　Sn=(a1+an)n/2

　等差数列求和公式

　Sn=na1+n(n-1)d/2; (d为公差)

　Sn=An2+Bn; A=d/2,B=a1-(d/2)

　和为 Sn

　首项 a1

　末项 an

　公差d

　项数n

　表示方法

　等差数列基本公式:

　末项=首项+(项数-1)?公差

　项数=(末项-首项)?公差+1

　首项=末项-(项数-1)?公差

　和=(首项+末项)?项数?2

　差:首项+项数?(项数-1)?公差?2

　说明

　末项:最后一位数

　首项:第一位数

　项数:一共有几位数

　和:求一共数的总和

　本段通项公式

　首项=2?和?项数-末项

　末项=2?和?项数-首项

　末项=首项+(项数-1)?公差:a1+(n-1)d

　项数=(末项-首项)/ 公差+1 :n=(an-a1)/d+1

　公差= d=(an-a1)/n-1

　如：1+3+5+7+?99 公差就是3-1

　将a1推广到am，则为:

　d=(an-am)/n-m

　基本性质

　若 m、n、p、q?N

　①若m+n=p+q，则am+an=ap+aq

　②若m+n=2q，则am+an=2aq(等差中项)

由前面推导可知，即由题设可知根的判别式=16(4K^2-m^2+1)>0，后面又求得k=-(m+1)/2

这样将k代入进去，4K^2-m^2+1>0

4ⅹ[-(m+1)/2]^2-m^2+1>0

化简得2m+2>0得m>-1

所以当且仅当m>-1时，根的判别式﹥0就是这样得来的。