深圳市历年高考,深圳市历年高考人数

1.2019年广东深圳市高考状元,广东深圳市文科理科高考状元姓名学校和分数

2.急求历届深圳市文科类高考试题！！！！谢谢帮忙！！guoxin0011@sina.com

3.深圳市各校高中高考升学率是多少

4.深圳市布吉高级中学历年的高考成绩怎么样？

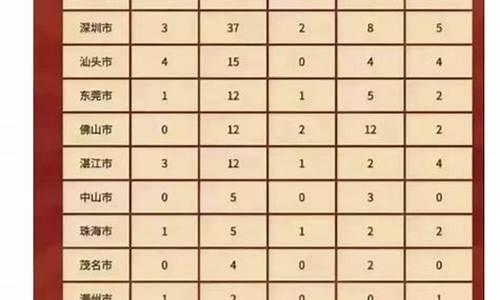
5万人左右。查询深圳市招考办显示，深圳每年高考人数较多，达到了5万左右，深圳高考生父亲或母亲应持有广东省居住证（在深圳报考的提交《深圳市居住证》)，有效期截止至当年高考报名规定时间，已连续3年以上(含3年)才可具备在深圳高考的资格。

2019年广东深圳市高考状元,广东深圳市文科理科高考状元姓名学校和分数

73%。据查询深圳教育局官网，2018年深圳高考本科录取率73%，中考录取率只有46.5%。深圳市，简称“深”，别称鹏城，广东省辖地级市，副省级市，国家计划单列市，超大城市，批复确定的中国经济特区、全国性经济中心城市和国际化城市。

急求历届深圳市文科类高考试题！！！！谢谢帮忙！！guoxin0011@sina.com

广东深圳市高考状元,广东深圳市文科理科高考状元姓名学校和分数

高考倒计时已经不足50天了，在这么短的备考时光里头，高三党及高考家长应该怎么做？高分网高考频道我分享深圳高考文科状元许思佳的经验给大家参考，她的爸爸也分享了一些经验供高考家长参考。

许思佳：深圳高考文科状元，她的父亲许辉一起谈论对孩子的教育经验。

丁时照：深圳报业集团副总编辑、深圳晚报总编辑，客串主持人

最后冲刺阶段要整理知识点往脑袋里填充

据悉，丁时照16岁时从湖北麻城第三中学进入 复旦大学 新闻系学习，是优秀的少年大学生。作为去年深圳高考文科状元，许思佳现就读于清华大学。这场“老学霸”与“小学霸”的对话看点十足。

丁时照：以你自己的亲身经历来看，你是怎么准备高考的?你对即将要上“战场”的学弟学妹有什么建议?

许思佳：这个时间离高考还有不到两个月，是一个要把知识点往脑袋里填充的过程。你要把一些不熟的，或者一些掌握的不太好的知识点整理到一个本子上。其实，我在高考最后冲刺的这段时间，也是每天早上5点半起来背书，晚上常常复习到12点才睡觉。

学弟学妹们一定要充分利用学习时间，一定要跟上老师的节奏，因为老师在备考经验上跟我们相比还是有很大优势的，不能只是按照自己的节奏埋头苦学。

丁时照：给台下的学弟学妹有什么建议?主要是在临考前的心理调整上。

许思佳：这段时间考试特别多，面对这些考试，考生一定要调整好心态，如果调整不过来，很容易出现厌学或浮躁情绪，都是不利于复习的。所以大家不要太较真每次考试，要不断告诉自己，就算这些考试考砸了又怎样，又不是高考。高考前的所有考试都是为了高考的“练兵”。

丁时照：饮食有什么要注意的吗?

许思佳：高三时候因为住校，也是正常吃饭堂。每周末回去，可能爸妈会把菜做得丰富些。

丁时照：许爸爸能培养出许思佳这样的学霸，也是一枚“神爸”。听说许思佳还有一个妹妹在读二年级，但是做四年级的题也是一点问题都没有。请我们的许爸爸来分享一下是如何教育孩子的?

许思佳爸爸许辉：去年这个时候，我跟台下所有的家长心情一样，但现在我坐在这里却觉得很平静。我认为家长在这段时间应该做好几件事情：

一、周末孩子回到家的时候一定要保障“后勤”服务；

二、家长一定要有一颗平常心。什么是平常心呢?现在小孩压力很大，他回来的时候，家长也会变得很紧张，如果小孩唉声叹气，作为家长一定要给孩子非常正面和积极的心理暗示，将正能量传递给孩子，这是非常重要的。许思佳高考的时候，我们还是照常晚上去散步，家长要学会帮孩子卸下压力。

深圳市各校高中高考升学率是多少

2009年普通高等学校招生全国统一考试(广东卷)

数学(文科）

本试卷共4页，21小题，满分150分。考试用时120分钟。

注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。用2B铅笔将试卷类型(A)填涂在答题卡相应位置上。将条形码横贴在答题卡右上角“条形码粘贴处”。

2．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。不按以上要求作答的答案无效。

4．作答选做题时，请先用2B铅笔填涂选做题的题号对应的信息点，再作答。漏涂、错涂、多涂的，答案无效。

5．考生必须保持答题卡的整洁。考试结束后，将试卷和答题卡一并交回。

参考公式：锥体的体积公式 ，其中 是锥体的底面积， 是锥体的高．

一、选择题：本大题共10 小题，每小题5分，满分50分.每小题给出得四个选项中，只有一项十符合题目要求得.

1.已知全集U=R，则正确表示集合M= {－1，0，1} 和N= { x |x +x=0} 关系的韦恩（Venn）图是

2.下列n的取值中，使 =1(i是虚数单位）的是

A. n=2 B. n=3 C. n=4 D. n=5

3.已知平面向量a= ，b= ， 则向量

A平行于 轴 B.平行于第一、三象限的角平分线

C.平行于 轴 D.平行于第二、四象限的角平分线

4.若函数 是函数 的反函数，且 ，则

A． B． C． D．2

5.已知等比数列 的公比为正数，且 ? =2 ， =1，则 =

A. B. C. D.2

6.给定下列四个命题：

①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；

②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；

③垂直于同一直线的两条直线相互平行；

④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.

其中，为真命题的是

A．①和② B．②和③ C．③和④ D．②和④

7.已知 中， 的对边分别为a,b,c若a=c= 且 ，则b=

A.2 B．4＋ C．4— D．

8.函数 的单调递增区间是

A. B.(0,3) C.(1,4) D.

9．函数 是

A．最小正周期为 的奇函数 B. 最小正周期为 的偶函数

C. 最小正周期为 的奇函数 D. 最小正周期为 的偶函数

10．广州2010年亚运会火炬传递在A、B、C、D、E五个城市之间进行，各城市之间的路线距离（单位：百公里）见下表.若以A为起点，E为终点，每个城市经过且只经过一次，那么火炬传递的最短路线距离是

A. B.21 C.22 D.23

二、填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分。

（一）必做题（11－13题）

11.某篮球队6名主力队员在最近三场比赛中投进的三分球个数如下表所示：

队员i 1 2 3 4 5 6

三分球个数

图1是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图，则图中判断框应填 ，输出的s=

(注：框图中的赋值符号“=”也可以写成“←”或“：=”)

图1

12．某单位200名职工的年龄分布情况如图2，现要从中抽取40名职工作样本，用系统抽样法，将全体职工随机按1－200编号，并按编号顺序平均分为40组（1－5号，6－10号…，196－200号）.若第5组抽出的号码为22，则第8组抽出的号码应是 。若用分层抽样方法，则40岁以下年龄段应抽取 人.

图 2

13．以点（2， ）为圆心且与直线 相切的圆的方程是 .

(二)选做题（14、15题，考生只能从中选做一题）

14．（坐标系与参数方程选做题）若直线 （t为参数）与直线 垂直，则常数 = .

15.(几何证明选讲选做题)如图3，点A、B、C是圆O上的点，且AB=4， ，则圆O的面积等于 .

图3

三、解答题，本大题共6小题，满分80分。解答须写出文字说明、证明过程和演算步骤。

16.（本小题满分12分）

已知向量 与 互相垂直，其中

（1）求 和 的值

（2）若 ， ,求 的值

17.（本小题满分13分）

某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P－EFGH,下半部分是长方体ABCD－EFGH.图5、图6分别是该标识墩的正(主)视图和俯视图.

（1）请画出该安全标识墩的侧(左)视图

（2）求该安全标识墩的体积

（3）证明:直线BD 平面PEG

18.（本小题满分13分）

随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.

(1)根据茎叶图判断哪个班的平均身高较高;

(2)计算甲班的样本方差

(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.

19.（本小题满分14分）

已知椭圆G的中心在坐标原点,长轴在 轴上,离心率为 ,两个焦点分别为 和 ,椭圆G上一点到 和 的距离之和为12.圆 : 的圆心为点 .

(1)求椭圆G的方程

(2)求 的面积

(3)问是否存在圆 包围椭圆G?请说明理由.

20.（本小题满分14分）

已知点（1， ）是函数 且 ）的图象上一点，等比数列 的前n项和为 ,数列 的首项为c，且前n项和 满足 － = + （n 2）.

（1）求数列 和 的通项公式；

（2）若数列{ 前n项和为 ，问 > 的最小正整数n是多少?

21.（本小题满分14分）

已知二次函数 的导函数的图像与直线 平行,且 在 =－1处取得最小值m－1(m ).设函数

(1)若曲线 上的点P到点Q(0,2)的距离的最小值为 ,求m的值

(2) 如何取值时,函数 存在零点,并求出零点.

参考答案

一、

1. B 2. C 3. C 4. A 5. B 6. D 7.A 8. D 9．A 10．B

二、

11. ,

12． 37, 20

13．

14．

15.

16.

解析（1） , ,即

又∵ , ∴ ,即 ,∴

又 ,

(2) ∵

, ,即

又 , ∴

17.

解析(1)侧视图同正视图,如下图所示.

（2）该安全标识墩的体积为：

（3）如图,连结EG,HF及 BD，EG与HF相交于O,连结PO.

由正四棱锥的性质可知, 平面EFGH ,

又 平面PEG

又 平面PEG；

18.

解析（1）由茎叶图可知：甲班身高集中于 之间，而乙班身高集中于 之间。因此乙班平均身高高于甲班;

(2)

甲班的样本方差为

＝57

（3）设身高为176cm的同学被抽中的事件为A；

从乙班10名同学中抽中两名身高不低于173cm的同学有：（181，173） （181，176）

（181，178） （181，179） （179，173） （179，176） （179，178） （178，173）

(178, 176) （176，173）共10个基本事件，而事件A含有4个基本事件；

；

19.解析（1）设椭圆G的方程为： （ ）半焦距为c;

则 , 解得 ,

所求椭圆G的方程为： .

(2 )点 的坐标为

（3）若 ，由 可知点（6，0）在圆 外，

若 ，由 可知点（-6，0）在圆 外；

不论K为何值圆 都不能包围椭圆G.

20.解析（1） ,

, ,

.

又数列 成等比数列， ，所以 ；

又公比 ，所以 ；

又 , , ；

数列 构成一个首相为1公差为1的等差数列， ，

当 ， ；

( )；

（2）

；

由 得 ，满足 的最小正整数为112.

21.解析（1）设 ，则 ；

又 的图像与直线 平行

又 在 取极小值， ，

， ；

， 设

则

；

（2）由 ，

得

当 时，方程 有一解 ，函数 有一零点 ；

当 时，方程 有二解 ，若 ， ，

函数 有两个零点 ；若 ，

，函数 有两个零点 ；

当 时，方程 有一解 , , 函数 有一零点

2008年普通高等学校招生全国统一考试（广东卷）

数学（文科）

一、选择题:本大题共10小题，每小题5分，满分50分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1、第二十九届夏季奥林匹克运动会将于2008年8月8日在北京举行，若集合A＝{参加北京奥运会比赛的运动员}，集合B={参加北京奥运会比赛的男运动员}，集合C={参加北京奥运会比赛的女运动员}，则下列关系正确的是（ ）

A、 B、 C、 D、

2、已知 ，复数 ，则 的取值范围是（ ）

A、（1，5） B、（1，3） C、（1， ） D、（1， ）

3、已知平面向量， ，且 // ，则 ＝（ ）

A、 B、 C、 D、

4、记等差数列的前 项和为 ，若 ，则该数列的公差 （ ）

A、2 B、3 C、6 D、7

5、已知函数 ，则 是（ ）

A、最小正周期为 的奇函数 B、最小正周期为 的奇函数

C、最小正周期为 的偶函数 D、最小正周期为 的偶函数

6、经过圆 的圆心C，且与直线 垂直的直线方程是（ ）

A、 B、 C、 D、

7、将正三棱柱截去三个角（如图1所示A、B、C分别是 三边的中点）得到的几何体如图2，则该几何体按图2所示方向的侧视图（或称左视图）为

8、命题“若函数 在其定义域内是减函数，则 ”的逆否命题是（ ）

A、若 ，则函数 在其定义域内不是减函数

B、若 ，则函数 在其定义域内不是减函数

C、若 ，则函数 在其定义域内是减函数

D、若 ，则函数 在其定义域内是减函数

9、设 ，若函数 ， ，有大于零的极值点，则（ ）

A、 B、 C、 D、

10、设 ，若 ，则下列不等式中正确的是（ ）

A、 B、 C、 D、

二、填空题

（一）必做题

11、为了调查某厂工人生产某种产品的能力，随机抽查了20位工人某天生产该产品的数量，产品数量的分组区间为 ， ， ， ， ，由此得到频率分布直方图如图3，则这20名工人中一天生产该产品数量在 的人数是 。

12、若变量 满足 ，则 的最大值是 。

13、阅读图4的程序框图，若输入 则输出 ， 。（注：框图中的赋值符号“＝”也可以写成“ ”或“ ”

（二）选做题（14~15题，考生只能从中选做一题）

14、（坐标系与参数方程选做题）已知曲线 的极坐标方程分别为 ，则曲线 交点的极坐标为 。

15、（几何证明选讲选做题）已知 是圆O的切线，切点为A，PA=2，AC是圆O的直径，PC与圆O交于B点，PB＝1，则圆O的半径R＝ 。

三、解答题：本大题共6小题，满分80分，解答须写出文字说明、证明过程和演算步骤。

16、已知函数 的最大值是1，其图像经过点 。

（1）求 的解析式；

（2）已知 ，且 求 的值。

17、某单位用2160万元购得一块空地，计划在该地块上建造一栋至少10层、每层2000平方米的楼房，经测算，如果将楼房建为 层，则每平方米的平均建筑费用为 （单位：元），为了使楼房每平方米的平均综合费用最少，该楼房应建为多少层？

（注：平均综合费用＝平均建筑费用+平均购地费用，平均购地费用＝ ）

18、如图5所示，四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形，其中BD是圆的直径， 。

（1）求线段PD的长；

（2）若 ，求三棱锥P-ABC的体积。

19、某初级中学共有学生2000名，各年级男、女生人数如下表：

初一年级 初二年级 初三年级

女生 373

男生 377 370

已知在全校学生中随机抽取1名，抽到初二年级女生的概率是0.19.

（1）求 的值；

（2）现用分层抽样的方法在全校抽取48名学生，问应在初三年级抽取多少名？

（3）已知 ，求初三年级中女生比男生多的概率。

20.设 ，椭圆方程为 ，抛物线方程为 如图6所示，过点 作 轴的平行线，与抛物线在第一象限的交点为G，已知抛物线在点G的切线经过椭圆的右焦点 。

（1）求满足条件的椭圆方程和抛物线方程；

（2）设A，B分别是椭圆长轴的左、右端点，试探究在抛物线上是否存在点P,使得 为直角三角形？若存在，请指出共有几个这样的点？并说明理由（不必具体求出这些点的坐标）。

21、设数列 满足 ， ， 。数列 满足 是非零整数，且对任意的正整数 和自然数 ，都有 。

（1）求数列 和 的通项公式；

（2）记 ，求数列 的前 项和 。

2008年普通高等学校招生全国统一考试（广东卷）

数学（文科）参考答案

一、选择题：

题号 1 2 3 4 5 6 7 8 9 10

答案 C C B B D C A A A D

二、填空题：

题号 11 12 13 14 15

答案 13 70 12、2

三、解答题：

16解：（1）依题意知A=1

，又 ；

∴ 即

因此 ；

（2）∵

且

∴

；

17、解：设楼房每平方米的平均综合费为f(x)元，则

(x≥10，x∈Z+)

令f?(x)=0 得 x=15

当x>15时，f?(x)>0；当0<x<15时，f?(x)<0

因此 当x=15时，f(x)取最小值f(15)=2000；

答：为了楼房每平方米的平均综合费最少，该楼房应建为15层。

18、解：（1）∵BD是圆的直径

∴∠BAD=90? 又△ADP~△BAD

∴

（2）在Rt△BCD中，CD=BDcos45?= R

∵PD2+CD2=9R2+2R2=11R2=PC2

∴PD⊥CD 又 ∠PDA=90?

∴PD⊥底面ABCD

S△ABC= AB×BC sin(60?+45?)= R× R = R2

三棱锥P-ABC的体积为

19、解：（1）∵

∴x=380

（2）初三年级人数为y+z=2000-(373+377+388+370)=500，

现用分层抽样的方法在全校抽取48名学生，应在初三年级抽取的人数为：

×500=12名

（3）设初三年级女生比男生多的事件为A，初三年级女生男生数记为(y,z)：

由（2）知y+z=500，且y,z∈N，

基本事件空间包含的基本事件有：

(245,255)、(246,254)、(247,253)、……(255,245)共11个

事件A包含的基本事件有：(251,249)、(252,248)、(253,247)、(254,246)、(255,245)共5个

∴P(A)= ；

20、解：（1）由x2=8(y-b)得 y= x2+b

当y=b+2时，x=±4，∴G点的坐标为(4,b+2)

，

过点G的切线方程为y-(b+2)=x-4，即y=x+b-2

令y=0得x=2-b，∴F1点的坐标为(2-b,0)；

由椭圆方程得F1点的坐标为(b,0)，

∴2-b=b 即b=1

因此所求的椭圆方程及抛物线方程分别为 和x2=8(y-1)

（2）∵过A作x轴的垂线与抛物线只有一个交点P，

∴以∠PAB为直角的Rt△ABP只有一个；

同理以∠PBA为直角的Rt△ABP只有一个；

若以∠APB为直角，设P点的坐标为(x, x2+1)，则A、B坐标分别

为 、

由 × =x2-2+( x2+1)2=0得 ，

关于x2的一元二次方程有一解，∴x有二解，即以∠APB为直角的Rt△ABP有二个；

因此抛物线上共存在4个点使△ABP为直角三角形。

21、解：（1）由 得 (n≥3)

又a2-a1=1≠0，

∴数列{an+1-an}是首项为1公比为 的等比数列，

an=a1+(a2-a1)+(a3-a2)+(a4-a3)+…+(an-an-1)

= ，

由 得b2=-1，由 得b3=1，…

同理可得当n为偶数时，bn=-1；当n为奇数时，bn=1；

因此bn=

（2）

Sn=c1+c2+c3+c4+…+cn

当n为奇数时，

=

当n为偶数时

=

令Tn= ……①

①× 得： Tn= ……②

①-②得： Tn =

= ∴Tn =

因此Sn=

2007年普通高等学校招生全国统一考试(广东卷)

数学(文科)

本试卷共4页，21小题，满分150分。考试用时l20分钟。

注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。用2B铅笔将试卷类型(A)填涂在答题卡相应位置上。将条形码横贴在答题卡右上角“条形码粘贴处”。

2．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目选项的答案信息点

涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3．非选择题必须用黑色宁迹钢笔或签字笔作答，答案必须写在答题卡各题目指

定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。不按以上要求作答的答案无效。

4．作答选做题时，请先用2B铅笔填涂选做题的题号(或题组号)对应的信息点，再作答。漏涂、错涂、多涂的，答案无效。

5．考生必须保持答题卡的整洁。考试结束后，将试卷和答题卡一并交回。

参考公式：锥体的体积公式 ，其中 是锥体的底面积， 是锥体的高．

如果事件 、 互斥，那么 ．

用最小二乘法求线性同归方程系数公式

一、选择题：本大题共l0小题，每小题5分，满分50分．在每小题给出的四个选项中。只有一项是符合题目要求的。

1．已知集合M={x| }，N={x| }，则M∩N=

A．{x|-1≤x＜0} B．{x |x>1}

C．{x|-1＜x＜0} D．{x |x≥-1}

2．若复数 是纯虚数( 是虚数单位， 是实数)，则

A．-2 B． C. D．2

3．若函数 ( )，则函数 在其定义域上是

A．单调递减的偶函数 B.单调递减的奇函数

C．单凋递增的偶函数 D.单涮递增的奇函数

4．若向量 、 满足| |=| |=1， 与 的夹角为 ，则 +

A． B． C. D．2

5．客车从甲地以60km／h的速度匀速行驶1小时到达乙地，在乙地停留了半小时，然后以

80km／h的速度匀速行驶l小时到达丙地。下列描述客车从甲地出发，经过乙地，最后到达 丙地所经过的路程s与时间t之间关系的图象中，正确的是

6若l、m、n是互不相同的空间直线，n、口是不重合的平面，则下列命题中为真命题的是

A．若 ，则 B．若 ，则

C. 若 ，则 D．若 ，则

7．图l是某县参加2007年高考的

学生身高条形统计图，从左到右

的各条形表示的学生人数依次记

为 、 、…、 (如

表示身高(单位： )在[150，

155)内的学生人数)．图2是统计

图l中身高在一定范围内学生人

数的一个算法流程图．现要统计

身高在160～180 (含

160 ，不含180 )的学生人

数，那么在流程图中的判断框内应填写的条件是

A． B． C． D．

8．在一个袋子中装有分别标注数字1，2，3，4，5的五个小球，这些小球除标注的数字外完全相同．现从中随机取出2个小球，则取出的小球标注的数字之和为3或6的概率是

A． B． C． D．

9．已知简谐运动 的图象经过点(0，1)，则该简谐运动的最小正周期 和初相 分别为

A． B． C． D．

10．图3是某汽车维修公司的维修点环形分布图公司在年初分配给A、

B、C、D四个维修点某种配件各50件．在使用前发现需将A、B、C、D

四个维修点的这批配件分别调整为40、45、54、61件，但调整只能在

相邻维修点之间进行．那么要完成上述调整，最少的调动件次( 件

配件从一个维修点调整到相邻维修点的调动件次为 )为

A．18 B．17 C．16 D．15

二、填空题：本大题共5小题，每小题5分，满分20分．其中14～15题是选做题，考生只能选做一题，两题全答的，只计算前一题得分．

11．在平面直角坐标系 中，已知抛物线关于 轴对称，顶点在原点 ，且过点P(2，4)，则该抛物线的方程是 ．

12．函数 的单调递增区间是 ．

13．已知数列{ }的前 项和 ，则其通项 ；若它的第 项满足 ，则 ．

14．(坐标系与参数方程选做题)在极坐标系中，直线 的方程为 ，则点 到直线 的距离为 ．

15．(几何证明选讲选做题)如图4所示，圆O的直径AB=6，C为圆周上一点， 过 作圆的切线 ，过A作 的垂线AD，垂足为D， 则∠DAC= ．

三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．

16．(本小题满分14分)

已知ΔABC三个顶点的直角坐标分别为A(3，4)、B(0，0)、C( ，0)．

(1)若 ，求 的值；

(2)若 ，求sin∠A的值．

17．(本小题满分12分)

已知某几何体的俯视图是如图5所示的矩形，正视图(或称主视图)是一个底边长为8、高为4的等腰三角形，侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形．

(1)求该几何体的体积V；

(2)求该几何体的侧面积S

18.(本小题满分12分)

下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的生产能耗 (吨标准煤)的几组对照数据

(1)请画出上表数据的散点图；

(2)请根据上表提供的数据，用最小二乘法求出 关于 的线性回归方程 ；

(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据(2)求出的线性同归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?

(参考数值： )

19.(本小题满分14分)

在平面直角坐标系 中，已知圆心在第二象限、半径为2／2的圆 与直线 相切于坐标原点 ．椭圆 与圆 的一个交点到椭圆两焦点的距离之和为 ．

(1)求圆 的方程；

(2)试探究圆 上是否存在异于原点的点 ，使 到椭圆右焦点F的距离等于线段 的长．若存在，请求出点 的坐标；若不存在，请说明理由．

20．(本小题满分14分)

已知函数 ， 、 是方程 的两个根( )， 是的导数

设 ， ， .

(1)求 、 的值；

(2)已知对任意的正整数 有 ,记 , .求数列{ }的

前 项和 ．

21．(本小题满分l4分)

已知 是实数，函数 ．如果函数 在区间 上有

零点，求 的取值范围．

2007年普通高考广东(文科数学)试卷(A卷)参考答案

一选择题: 1-10 CDBBC DBAAC

二填空题: 11. 12. 13. 2n-10 ; 8 14. 2 15.

三解答题:

16.解: (1)

由 得

(2)

17解: 由已知可得该几何体是一个底面为矩形,高为4,顶点在底面的射影是矩形中心的

四棱锥V-ABCD ;

(1)

(2) 该四棱锥有两个侧面VAD. VBC是全等的等腰三角形,且BC边上的高为

, 另两个侧面VAB. VCD也是全等的等腰三角形,

AB边上的高为

因此

18解: (1) 散点图略

(2)

;

所求的回归方程为

(3) ,

预测生产100吨甲产品的生产能耗比技改前降低 (吨)

19解:(1) 设圆C 的圆心为 (m, n)

则 解得

所求的圆的方程为

(2) 由已知可得

椭圆的方程为 , 右焦点为 F( 4, 0) ;

假设存在Q点 使 ,

整理得 代入 得:

,

因此不存在符合题意的Q点.

20解:(1) 由 得

(2)

又

数列 是一个首项为 ,公比为2的等比数列;

21解: 若 , ,显然在上没有零点, 所以

令 得

当 时, 恰有一个零点在 上;

当 即 时, 也恰有一个零点在 上;

当 在 上有两个零点时, 则

或

解得 或

因此 的取值范围是 或 ;

深圳市布吉高级中学历年的高考成绩怎么样？

深圳市各校高中高考升学率如下：

1、深圳中学2022年参加高考人数为675人，其中物理类考生602人，历史类考生73人，中山大学上线率：72%，华南理工大学上线率：74.2%。

2、深圳实验学校2022年参加高考人数为492人，985、211、双一流大学录取率达80%（不含香港及出国），211大学上线率近100%。

3、深圳外国语学校2022年高考特控率99%，中大线70%。

4、深圳高级中学2022年高考特控上线率98%，本科上线率100%。

5、深圳宝安中学2022年特控线达标率93.3%（物理类93.1%，历史类94.7%），本科达线率99.9%。

6、深圳大学附属中学2022年高考特控率94%。

7、翠园中学2022届高考特控线上线率82.91%，本科率100%。

深圳市布吉高级中学历年的高考成绩还行。高考满分大部分省市满分为750分。

深圳市布吉高级中学坐落在全国著名文明村——南岭村社区，毗邻全国文化产业基地——大芬油画村。

广东省一级学校，龙岗区直属重点高中，龙岗区十一五规划中创建“国家级示范高中”推荐学校，全国普通高考定点考场。学校占地60539平方米，建筑面积59801平方米，环境幽雅。

学校简介：

深圳市布吉高级中学坐落在全国文明村——南岭村社区，毗邻全国文化产业基地——大芬油画村，全国普通深圳市布吉高级中学。

高考定点考场，广东省高中教育教学优秀学校，广东省绿色学校，龙岗区直属高中，2007年9月顺利通过国家级示范性高中初期督导验收。

以上内容参考：百度百科——深圳市布吉高级中学