1.高考的数学考点有哪些？

2.三道关于解三角形的高一数学问题

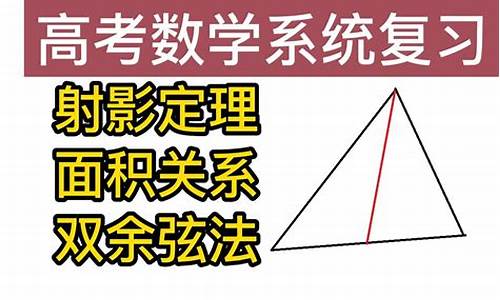
高考解三角形_高考解三角形大题

这是高中题目？证明感觉是初中题目呢？

主要利用相似性质

过点E作EF⊥BC，设EF=x，因为∠ADC=EDB=π/4，DB=√2，那么FB=√2-x

那么FB/BC=BE/AB=EF/AC，√2-x/BC=BE/AB=1/4，所以BC=4（√2-x），CD=3√2-4x

而AC=4x，即AC=CD，所以3√2-4x=4x，x=3√2/8，所以AC=3√2/2

高考的数学考点有哪些？

其实是这样的，为什么第1例用余弦定理求钝角三角形的时候，结果正确；而第2例求锐角三角形的时候，结果不正确。

首先长边对大角。所以钝角三角形中，最长的边对应最大的角---钝角。在你的第一个例子中，三个边的关系已经确定，是2a+1最大。所以这条边对应的角就必然是钝角。然后根据这个角的余弦就能求出a的范围。而且应该是a>2和1<a<8并集2<a<8。

但是第二例中，x和3的大小关系不确定。所以到底是x边对应的角大，还是3对应的角大不确定。锐角三角形必须三个角都是锐角；也就是说必须最大的角是锐角。所以必须对x对应的边是锐角用余弦定理求一次，对3对应的边用余弦定理也求一次。两次不等式求出来的结果的并集才是所要求的结果。

而如果类似第二例中，边长是2、3、x的钝角三角形，求x的取值范围。那么你如果单纯对x对应的角用余弦定理求，结果也会不正确。因为有可能是3对应的角是钝角。

所以你的总结并不对。第1例结果正确的原因不在于是求的钝角三角形，而在于三个边的大小关系已经确定。第2力之所以错误的原因不在于是求锐角三角形，而在于有两个边3和x的大小关系没确定。

三道关于解三角形的高一数学问题

高考的数学考点有：

1、数列＆解三角形

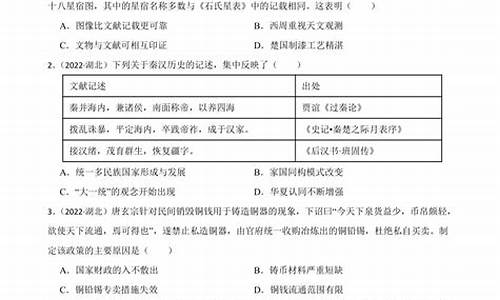
数列与解三角形的知识点在解答题的第一题中，是非此即彼的状态，近些年的特征是大题第一题两年数列两年解三角形轮流来，2014、2015年大题第一题考查的是数列，2016年大题第一题考查的是解三角形，故预计2017年大题第一题较大可能仍然考查解三角形。

数列主要考察数列的定义，等差数列、等比数列的性质，数列的通项公式及数列的求和。解三角形在解答题中主要考查正、余弦定理在解三角形中的应用。

2、立体几何

高考在解答题的第二或第三题位置考查一道立体几何题，主要考查空间线面平行、垂直的证明，求二面角等，出题比较稳定，第二问需合理建立空间直角坐标系，并正确计算。

3、概率

高考在解答题的第二或第三题位置考查一道概率题，主要考查古典概型，几何概型，二项分布，超几何分布，回归分析与统计，近年来概率题每年考查的角度都不一样，并且题干长，是学生感到困难的一题，需正确理解题意。

4、解析几何

高考在第20题的位置考查一道解析几何题。主要考查圆锥曲线的定义和性质，轨迹方程问题、含参问题、定点定值问题、取值范围问题，通过点的坐标运算解决问题。

5、导数

高考在第21题的位置考查一道导数题。主要考查含参数的函数的切线、单调性、最值、零点、不等式证明等问题，并且含参问题一般较难，处于必做题的最后一题。

1.

a=4，b=3，C=60°

c^2=a^2+b^2-2abcosC=4^2+3^2-2*4*3*1/2 = 13

c=√13

sinA=asinC/c = 4*√3/2 /√13 = 2√39 /13

2.

b^2=ac

b^2=a^2+c^2-2accosB

ac=a^2+c^2-2accosB

cosB = (a^2+c^2-ac)/(2ac) = (a^2+c^2)/(2ac) - 1/2

∵(a-c)^2≥0，a^2+c^2≥2ac，(a^2+c^2)/(2ac) ≥ 1

∴cosB = (a^2+c^2)/(2ac) - 1/2 ≥ 1/2

∴0＜B ≤ 60°

3.

(b+c):(c+a):(a+b)=12:8:10

(b+c)/(c+a)=12/8，(b/c+1)/(1+a/c)=3/2，2b/c-3a/c=1 ... (1)

(c+a)/(a+b)=8/10，(1+a/c)/(a/c+b/c)=4/5，4b/c-a/c=5 ...(2）

(2)-(1)*2得：5a/c=3，a/c = 3/5

4b/c=5+a/c=5+3/5=28/5，b/c=7/5

cosB = (a^2+c^2-b^2)/(2ac)

= { (a/c)^2 + 1 - (b/c)^2 } / (2a/c)

= { (3/5)^2 + 1 - (7/5)^2 } / (2*3/5)

= ( 3^2 + 5^2 - 7^2 ) / (2*3*5)

= -15/30

= -1/2

B=120°