数学高考立体几何大题,数学高考立体几何

1.福建省文科数学高考共建立体几何用向量的方法给分不？

2.高中文科数学立体几何怎么学

3.高考数学中的立体几何题怎样建立坐标系？

4.高考数学立体几何评分标准及评分细则

5.高考数学立体几何得分标准_数值错误的扣分

6.立体几何求角方法

当然重要，高考立体几何占20-30分，而且必出大题。立体几何难，是因为很多人特别是女生，从小没有培养训练过立体几何思维，如果立体思维哈，立体几何其实是最简单的初中平面几何！ 立体几何思维只能通过学习研究立体几何模型来培养啊，去买立体几何模型，是明智的选择。

福建省文科数学高考共建立体几何用向量的方法给分不？

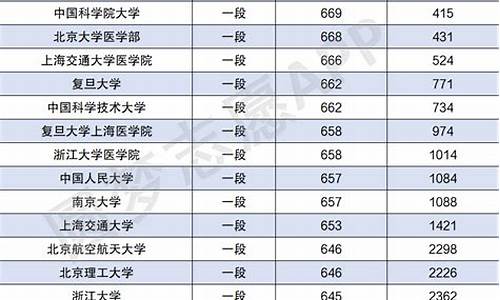
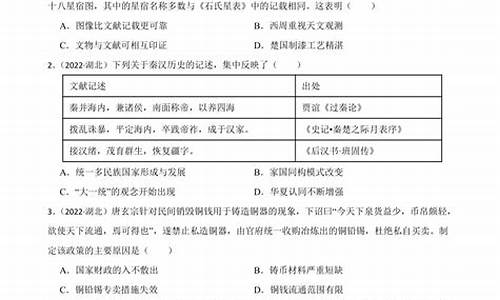
一般是一道选择5分，一道填空5分，一道大题12分共22分。但根据历年高考命题专家思路不同可能稍有差异，如09年全国卷一选择题第9（三棱柱问题)，第11道题(二面角问题），填空第15道题（球类问题）以及大题第18道（四棱锥问题）合计27分。至于10年试题所占比重等今年的《考试大纲》出来之后就知道了，不过一般变动不大。

立体几何中占分值最大的要数“求空间角与空间距离”这一块，但凡立体几何大都能用向量法解，这对文科生来说也算是学习立体几何的一个捷径吧，尤其是在高三冲刺阶段只要掌握住用向量法解立体几何，几乎都可以做出啦。另外高中数学中真正的难点是在解析几何一章，高考占分较重且无论选择填空还是大题都多以压轴题出现，文科生得数学者的天下，所以希望你能注意这一点！！！最后预祝你能取得好成绩，考上理想的大学。

高中文科数学立体几何怎么学

给分

但空间向量有特殊之处，如果高考题出的巧那么就很难建出来

空间向量没有步骤分，坐标算对了给分，没得出结果那一小问直接没分

而且你注意要区别左手系和右手系的问题

空间向量适合证不显著甚至要添线的平行和垂直问题

高考数学中的立体几何题怎样建立坐标系？

这应该是高中数学的附加题吧，（1）用基本方法，建系，找点坐标，代入计算。。（2）做fo垂直于mn于o点，然后求fo，mo长，最后勾股定理。

以a为原点，以ab为x轴，以ad为y轴以ah垂直于平面abcd于a点为z轴。建立空间直角坐标系。

做mn，ef的垂直平分线，能得要一个交点，

所以a‘在abcd上的投影是交点

不好意思，我看错了，你再等等，我去画图

想到了，你画一个底面的图，因为ae=af，且a'在abcd投影在ef中点，做ef中点g，连接cg

因为a'能与c的翻折点重合，所以mn垂直于cg。所以mn平行于ef。

做gx垂直于mn于x点，gx=两平行线距离，从m向n看，a'gx是个直角三角形

gx方=a'x方-a'g方，因为a’x=xc,ag

gx

xc=2*根号41，然后二元一次方程求gx长

最后能从俯视图里看出gx与ad夹角为45°，fm=gx/cos45°

高考数学立体几何评分标准及评分细则

楼主问的这个问题太宽泛了，

总的来讲，立体几何中建立坐标系的方法有很多种，即使在一个题目中，也有很多种建立坐标系的方法，但是各个方法表示几何图形中点的坐标的难易是不一样的，所以一个好的坐标系选取的标准就是：想办法建立一个坐标系，在这个坐标系中，图形中点的坐标表示尽可能的简单，这样你的运算或者几何关系才会比较容易的得到。

有了这个标准，就可以视具体问题具体的建立合适的坐标系了，一般是先确定坐标原点，而坐标原点的选取多选择图形的中心或者某个顶点或者某一条边的中点，这样就会让图形中的点容易表示出来。更多的理解要结合具体例子体会，楼主不妨找几个例题做一下。

祝你学习进步！

高考数学立体几何得分标准_数值错误的扣分

高考数学立体几何评分标准评分及评分细则：

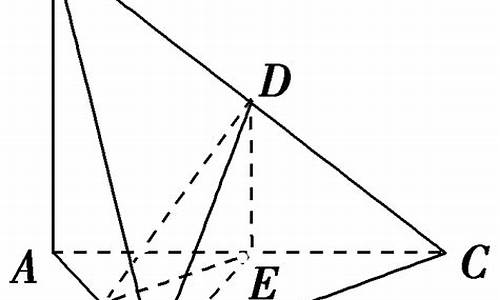
(2017全国3,文19)(本小题满分12分)如图,四面体ABCD中,△ABC是正三角形,AD=CD.

1.证明线面垂直时,不要忽视“面内两条直线为相交直线”这一条件,如第(1)问中,学生易忽视“DO∩BO=O”,导致条件不全而减分;

2.求四面体的体积时,要注意“等体积法”的应用,即合理转化四面体的顶点和底面,目的是底面积和顶点到底面的距离容易求得;

3.注意利用第(1)问的结果:在题设条件下,如果第(1)问的结果第(2)问能用得上,可以直接用,有些题目不用第(1)问的结果甚至无法解决,如本题中,由(1)及题设知∠ADC=90°.

4.要注意书写过程规范,计算结果正确.书写规范是计算正确的前提,在高考这一特定的环境下,学生更要保持规范书写,力争一次成功,但部分学生因平时习惯,解答过程中书写混乱,导致失误过多.

扩展资料：

高考数学立体几何解题方法：

坐标系法：一般是两步给分，一是各关键点的的坐标，二是结果。

几何法：按你所写的关键步骤分步给分。

二者各有优缺点，坐标系法简单方便，容易入手。但是如果结果算错了，得到的步骤分很少。几何法较难，但是结果算错了只要步骤对，也能得到大部分分值。

立体几何求角方法

1、两个二倍角公式，诱导公式，各给1分；

2、如果只有最后一步结果，没有过程，则给1分，不影响后续得分；

3、最后一步结果正确，但缺少上面的某一步过程，不扣分；

4、如果过程中某一步化简错了，则只给这一步前面的得分点。

扩展资料：

对于高考数学题，特点是压轴题，有很多同学抱着“回避”的态度，这种“回避”必然导致“起评分”降低－－别人从“150分”的试题中得分，而你只能从“120分”的试题中得分。

因此，从某种意义上说，这种“回避”增加了考试的难度！因为，假如有些基础题你思维“短路”，立刻导致考试“溃败”。

其实，只要我们了解高考数学题的特点，并且掌握一定的答题技巧，注意评分的细则，相信同学们还是能够取得高分的。下面，我谈一谈我的几点认识，供同学们参考。

高考数学立体几何大题中，有两类问题是最重要的。一是平行和垂直的证明；二是求角。求角问题又分为三类：1）求两异面直线所成的角。2）求线面角。3）求二面角。

方法：一是采用立体几何常规方法，按照线线角、线面角、二面角的定义把线线角、线面角、二面角的平面角找到，然后放到一个三角形中去计算；二是建立坐标系采用空间向量法去求角。

1、求两异面直线所成的角：角的范围是0度到90度，不包括0度，包括90度。方法是一条直线不动，另外一条直线平行移动到跟前一条直线相交，它们所成的锐角或直角为两异面直线所成的角，然后放入它的所在的三角形中去解三角形求出角的大小。当然也可以在几何体中另取一点，将两条直线都平行移动到相交，再去求角的大小。

遇到正方体对角线时，通常采用补形法在正方体旁补一个一模一样大小的正方体，然后再去平行移动直线。

易错点：若题设条件告诉你两异面直线所成的角，反回到图形中应有两种情况，这个角或它的补角。

2、求线面角：角的范围是0度到90度，不包括0度，包括90度。

方法有定义法、等体积法、补形法等。

等体积法模型：当过一个点作一个平面的垂线时，若垂足不好确定，则通过等体积法直接确定垂线段即高线的长度，然后将高线长放在一直角三角形中求角。