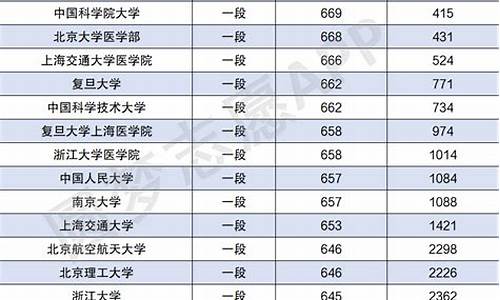
高考文科数学大纲-高考文科数学考试大纲

1.在线等 高三文科数学都有些什么内容

2.近几年高考全国2卷文科数学都考查哪些方面的知识点,都能占多少分。

3.高中文科数学第二轮复习大纲

4.高中的数学文理科有哪些区别？文理科数学难度差距大吗？

5.文科高考数学必背公式

在线等 高三文科数学都有些什么内容

如果只谈高三的内容的话就是个概论统计和导数，比较简单。

统计基本就是小题，主要是期望值、方差、标准差的计算。

导函数题型有几种典型多做几道就好，一般考察一元二次方程的导数运算以及极大极小值和最大最小值的计算，有些时候考应用题。

数学需要方法，我自己就深有体会。我的数学不是太好，但是高中数学部分比我好的应该找不出几个。

还在高中时，一份高考试卷，提前30分钟交卷，如果没有特殊情况的话，140多应该时没有问题的。现在自己试着带了几个学生，刚开始都是60，70那个模样的(总分150)，一两个月之后，一般的，也可以达到110~120这个模样，诀窍就是一个，方法。怎样才可以学好数学呢?

要想学好数学，其实很简单，注意下面几点就足够了:

1、不要怕数学

很多同学对数学似乎有一种天生的恐惧感，一看到数学，心里就自然而然的产生一种抗拒情绪，影响自己正常的思维。特别是那些应用题，有些同学连题目都没有看到，一看题目那么长，就不敢下笔，直接认为自己不会做，白白浪费了大好的机会。须不知，数学的应用题，实际上就是所谓的送分题，很少有真正的难点出现。只要你能够认真的把题目读完，写出数学表达式，分数就做完了一大半。

其实数学里面，大部分都是变化，真正要记的也就是那么几个公式。我们完全可以跟玩游戏一样，把他当作游戏来看待。数学公式就是我们手中的武器，题目就是我们的敌人。只是每一种武器都有它自己的特性。不同的敌人，可能要换多种武器而已。我想大家玩游戏时，应该不会看到敌人，还没有动手就逃跑吧。那样你早就翘翘了，还怎么通关呢?这个，也就是我把这个网站叫做游戏数学的目的。视数学为游戏，游戏而已，有什么大惊小怪的呢!真正碰壁了，换一条路就行了，走迷宫，我们都是高手。一个小小的数学题，就想让我们害怕，可能吗?

当然，要想真正的做到视数学为游戏这个地步，还需要一个坚实的基础，这就是数学的基础知识(在我网站里面，这个很详细)。你级数不够，连一个小兵都打不过，又凭什么去对付那个BOSS呢?

2、注意考场答题的技巧

有些同学特别厉害，每个题都一心一意的去做，但问题是他时间严重不够，光选择题就用了差不多一个小时，到后面做大题时，明明知道怎么做，也相信自己能够做出来，可惜已经快交卷了，只能忍痛舍弃。可怜啊，为什么刚开始的时候不注意呢?

首先，做考场数学题，特别是高考题，一定要注意答题的技巧。刚拿到试卷的时候，不要直接就动手做题(一般老师也不会允许你答题)，要好好把我这个时间，把整个试卷看一下(主要是看后面的几个大题目)，看一下有没有自己曾经做过的题目，或者是自己曾经见过那个题型，看一下有没有自己能够很快就可以做完的题目，看完之后，首先就把这些题目做出来。然后再做选择题。整个高考做题的步骤是这样的:曾经做过的题--选择题--大题--填空题。为什么把填空题放在最后呢，因为填空题分值较小，而且跟计算题区别不大，要费很大心思，它又不像选择题，可以猜答案，所以一般放在最后。

其次，做考场题的时候，一定要注意拿分。也就是说，做的一切都是为了分数。题目不会做不要紧，有分拿就OK了。所以做题时，特别是在做后面那些计算题的时候，要注意拿分的技巧。第一个要注意的就是解题格式。因为高考是按步骤给分的，所以，无论你那个题目会不会做，至少你要有一个题设过程，然后再写出一个数学式子(如果你数学式子写不出来，起码用中文写一个表达式是没有问题的吧)。至于计算，如果你实在不会，就算了，不要在这里浪费太多的时间，后面还有很多题目等着你呢!

3、注意做题技巧

这里讲的做题技巧，主要是针对选择题和填空题而言。这类题目，要的只是一个答案，至于用什么方法，没有任何要求。我们做的时候，没有必要象做计算题一样，老老实实的去计算。只要能够得到答案，就算是猜的，也没有人能够管你。所以这一类题目，要点就是一个:猜!我曾经和我的学生看了一下，找了好几份高考试卷，结果每一套试卷，都至少有50分以上的题目是不用计算的、

近几年高考全国2卷文科数学都考查哪些方面的知识点,都能占多少分。

选择题和填空题都是零散的知识点

没办法找到规律

但一般第一题是集合

大题一般是

立体几何

约12分

概率约12分

数列约12分

函数综合要18分左右

我个人认为函数

直线和

曲线方程

的综合比较重要

高中文科数学第二轮复习大纲

高中数学合集百度网盘下载

链接：提取码：1234

简介：高中数学优质资料下载，包括：试题试卷、课件、教材、视频、各大名师网校合集。

高中的数学文理科有哪些区别？文理科数学难度差距大吗？

高考文理科数学区别1：知识范围不同

首先是知识范围方面，两者使用的教科书是一样的，但是文科数学所需要的知识量要比理科数学少。一般文科数学高考时会考必修1-5，选修1-1，1-2，4-4或4-5这几本书；而理科数学高考时则一般会考必修1-5，选修2-1，2-2，2-3，4-4或4-5这几本书。

具体考点的不同，要看当年高考的考试大纲。但是文理科数学题目大样类似，有六成以上的题是一样的；一般第一题不一样，第一题一般理科考察虚数，文科不考；填空题可能理科会出现统计的问题，相对难一些；排列组合一般理科可能会多一问；最后一题问法会有区别，理科的难度大一些。

高考文理科数学区别2：难度不同

文理科数学即使是针对同一个考察点的考察，难度也是有很大不同的。对于基础题目文理科数学一般都是一样的。主要的差别在于一些中高档题目上。

文科题目的已知条件往往比理科题目直接，从而容易解答。另外理科有一些知识点文科是没有的，不过这个比较少。而且理科的数学要求高些，所学的知识有部分比文科更深入。所以从难易程度看，高考理科数学要难于高考文科数学。

1.圆锥曲线与方程

曲线与方程

顶点在坐标原点的抛物线的标准方程与几何性质

2.空间向量与立体几何

空间向量的概念

空间向量共线、共面的充分必要条件

空间向量的加法、减法及数乘运算

空间向量的坐标表示

空间向量的数量积

空间向量的共线与垂直

3.导数及其应用

简单的复合函数的导数

定积分

4.推理与证明

数学归纳法的原理

数学归纳法的简单应用

5.计数原理

加法原理与乘法原理

排列与组合

二项式定理

6.概率统计

离散型随机变量及其分布列

超几何分布

条件概率及相互独立事件

n次独立重复试验的模型及二项分布

离散型随机变量的均值与方差

7.几何证明选讲

相似三角形的判定与性质定理

射影定理

圆的切线的判定与性质定理

圆周角定理，弦切角定理

相交弦定理、割线定理、切割线定理

圆内接四边形的判定与性质定理

8.矩阵与变换

矩阵的概念

二阶矩阵与平面向量

常见的平面变换

矩阵的复合与矩阵的乘法

二阶逆矩阵

二阶矩阵的特征值和特征向量

二阶矩阵的简单应用

9.坐标系与参数方程

坐标系的有关概念

简单图形的极坐标方程

极坐标方程与直角坐标方程的互化

参数方程

直线、圆及椭圆的参数方程

参数方程与普通方程的互化

参数方程的简单应用

10.不等式选讲

不等式的基本性质

含有绝对值的不等式的求解

不等式的证明(比较法、综合法、分析法)

算术-几何平均不等式、柯西不等式

利用不等式求最大(小)值

运用数学归纳法证明不等式

文科高考数学必背公式

一、高中数学诱导公式全集：

常用的诱导公式有以下几组：

公式一：

设α为任意角，终边相同的角的同一三角函数的值相等：

sin（2kπ＋α）＝sinα （k∈Z）

cos（2kπ＋α）＝cosα （k∈Z）

tan（2kπ＋α）＝tanα （k∈Z）

cot（2kπ＋α）＝cotα （k∈Z）

公式二：

设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：

sin（π＋α）＝－sinα

cos（π＋α）＝－cosα

tan（π＋α）＝tanα

cot（π＋α）＝cotα

公式三：

任意角α与 -α的三角函数值之间的关系：

sin（－α）＝－sinα

cos（－α）＝cosα

tan（－α）＝－tanα

cot（－α）＝－cotα

公式四：

利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：

sin（π－α）＝sinα

cos（π－α）＝－cosα

tan（π－α）＝－tanα

cot（π－α）＝－cotα

公式五：

利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系：

sin（2π－α）＝－sinα

cos（2π－α）＝cosα

tan（2π－α）＝－tanα

cot（2π－α）＝－cotα

公式六：

π/2±α及3π/2±α与α的三角函数值之间的关系：

sin（π/2＋α）＝cosα

cos（π/2＋α）＝－sinα

tan（π/2＋α）＝－cotα

cot（π/2＋α）＝－tanα

sin（π/2－α）＝cosα

cos（π/2－α）＝sinα

tan（π/2－α）＝cotα

cot（π/2－α）＝tanα

sin（3π/2＋α）＝－cosα

cos（3π/2＋α）＝sinα

tan（3π/2＋α）＝－cotα

cot（3π/2＋α）＝－tanα

sin（3π/2－α）＝－cosα

cos（3π/2－α）＝－sinα

tan（3π/2－α）＝cotα

cot（3π/2－α）＝tanα

(以上k∈Z)

注意：在做题时，将a看成锐角来做会比较好做。

诱导公式记忆口诀

※规律总结※

上面这些诱导公式可以概括为：

对于π/2*k ±α(k∈Z)的三角函数值，

①当k是偶数时，得到α的同名函数值，即函数名不改变；

②当k是奇数时，得到α相应的余函数值，即sin→cos;cos→sin;tan→cot,cot→tan.

（奇变偶不变）

然后在前面加上把α看成锐角时原函数值的符号。

（符号看象限）

例如：

sin(2π－α)＝sin(4·π/2－α)，k＝4为偶数，所以取sinα。

当α是锐角时，2π－α∈(270°，360°)，sin(2π－α)＜0，符号为“－”。

所以sin(2π－α)＝－sinα

上述的记忆口诀是：

奇变偶不变，符号看象限。

公式右边的符号为把α视为锐角时，角k·360°+α（k∈Z），-α、180°±α，360°-α

所在象限的原三角函数值的符号可记忆

水平诱导名不变；符号看象限。

＃

各种三角函数在四个象限的符号如何判断，也可以记住口诀“一全正；二正弦(余割)；三两切；四余弦(正割)”．

这十二字口诀的意思就是说：

第一象限内任何一个角的四种三角函数值都是“＋”；

第二象限内只有正弦是“＋”，其余全部是“－”；

第三象限内切函数是“＋”，弦函数是“－”；

第四象限内只有余弦是“＋”，其余全部是“－”．

上述记忆口诀,一全正,二正弦,三内切,四余弦

＃

还有一种按照函数类型分象限定正负：

函数类型 第一象限 第二象限 第三象限 第四象限

正弦 ...........＋............＋............—............—........

余弦 ...........＋............—............—............＋........

正切 ...........＋............—............＋............—........

余切 ...........＋............—............＋............—........

同角三角函数基本关系

同角三角函数的基本关系式

倒数关系:

tanα ·cotα＝1

sinα ·cscα＝1

cosα ·secα＝1

商的关系：

sinα/cosα＝tanα＝secα/cscα

cosα/sinα＝cotα＝cscα/secα

平方关系：

sin^2(α)＋cos^2(α)＝1

1＋tan^2(α)＝sec^2(α)

1＋cot^2(α)＝csc^2(α)

同角三角函数关系六角形记忆法

六角形记忆法：（参看或参考资料链接）

构造以"上弦、中切、下割；左正、右余、中间1"的正六边形为模型。

（1）倒数关系：对角线上两个函数互为倒数；

（2）商数关系：六边形任意一顶点上的函数值等于与它相邻的两个顶点上函数值的乘积。

（主要是两条虚线两端的三角函数值的乘积）。由此，可得商数关系式。

（3）平方关系：在带有阴影线的三角形中，上面两个顶点上的三角函数值的平方和等于下面顶点上的三角函数值的平方。

两角和差公式

两角和与差的三角函数公式

sin（α＋β）＝sinαcosβ＋cosαsinβ

sin（α－β）＝sinαcosβ－cosαsinβ

cos（α＋β）＝cosαcosβ－sinαsinβ

cos（α－β）＝cosαcosβ＋sinαsinβ

tan（α＋β）＝(tanα+tanβ)／(1-tanαtanβ)

tan（α－β）＝(tanα－tanβ)／(1＋tanα·tanβ)

二倍角公式

二倍角的正弦、余弦和正切公式（升幂缩角公式）

sin2α＝2sinαcosα

cos2α＝cos^2(α)－sin^2(α)＝2cos^2(α)－1＝1－2sin^2(α)

tan2α＝2tanα/[1－tan^2(α)]

半角公式

半角的正弦、余弦和正切公式（降幂扩角公式）

sin^2(α/2)＝(1－cosα)／2

cos^2(α/2)＝(1＋cosα)／2

tan^2(α/2)＝(1－cosα)／(1＋cosα)

另也有tan(α/2)=(1－cosα)/sinα=sinα/(1+cosα)

万能公式

万能公式

sinα=2tan(α/2)/[1+tan^2(α/2)]

cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]

tanα=2tan(α/2)/[1-tan^2(α/2)]

万能公式推导

附推导：

sin2α=2sinαcosα=2sinαcosα/(cos^2(α)+sin^2(α))......*，

（因为cos^2(α)+sin^2(α)=1）

再把*分式上下同除cos^2(α)，可得sin2α＝2tanα/(1＋tan^2(α))

然后用α/2代替α即可。

同理可推导余弦的万能公式。正切的万能公式可通过正弦比余弦得到。

三倍角公式

三倍角的正弦、余弦和正切公式

sin3α＝3sinα－4sin^3(α)

cos3α＝4cos^3(α)－3cosα

tan3α＝[3tanα－tan^3(α)]／[1－3tan^2(α)]

三倍角公式推导

附推导：

tan3α＝sin3α/cos3α

＝(sin2αcosα＋cos2αsinα)/(cos2αcosα-sin2αsinα)

＝(2sinαcos^2(α)＋cos^2(α)sinα－sin^3(α))/(cos^3(α)－cosαsin^2(α)－2sin^2(α)cosα)

上下同除以cos^3(α)，得：

tan3α＝(3tanα－tan^3(α))/(1-3tan^2(α))

sin3α＝sin(2α＋α)＝sin2αcosα＋cos2αsinα

＝2sinαcos^2(α)＋(1－2sin^2(α))sinα

＝2sinα－2sin^3(α)＋sinα－2sin^3(α)

＝3sinα－4sin^3(α)

cos3α＝cos(2α＋α)＝cos2αcosα－sin2αsinα

＝(2cos^2(α)－1)cosα－2cosαsin^2(α)

＝2cos^3(α)－cosα＋(2cosα－2cos^3(α))

＝4cos^3(α)－3cosα

即

sin3α＝3sinα－4sin^3(α)

cos3α＝4cos^3(α)－3cosα

三倍角公式联想记忆

★记忆方法：谐音、联想

正弦三倍角：3元 减 4元3角（欠债了(被减成负数)，所以要“挣钱”(音似“正弦”)）

余弦三倍角：4元3角 减 3元（减完之后还有“余”）

☆☆注意函数名，即正弦的三倍角都用正弦表示，余弦的三倍角都用余弦表示。

★另外的记忆方法:

正弦三倍角: 山无司令 (谐音为 三无四立) 三指的是"3倍"sinα, 无指的是减号, 四指的是"4倍", 立指的是sinα立方

余弦三倍角: 司令无山 与上同理

和差化积公式

三角函数的和差化积公式

sinα＋sinβ＝2sin[(α＋β)/2]·cos[(α－β)/2]

sinα－sinβ＝2cos[(α＋β)/2]·sin[(α－β)/2]

cosα＋cosβ＝2cos[(α＋β)/2]·cos[(α－β)/2]

cosα－cosβ＝－2sin[(α＋β)/2]·sin[(α－β)/2]

积化和差公式

三角函数的积化和差公式

sinα ·cosβ＝0.5[sin(α＋β)＋sin(α－β)]

cosα ·sinβ＝0.5[sin(α＋β)－sin(α－β)]

cosα ·cosβ＝0.5[cos(α＋β)＋cos(α－β)]

sinα ·sinβ＝－0.5[cos(α＋β)－cos(α－β)]

和差化积公式推导

附推导：

首先,我们知道sin(a+b)=sina*cosb+cosa*sinb,sin(a-b)=sina*cosb-cosa*sinb

我们把两式相加就得到sin(a+b)+sin(a-b)=2sina*cosb

所以,sina*cosb=(sin(a+b)+sin(a-b))/2

同理,若把两式相减,就得到cosa*sinb=(sin(a+b)-sin(a-b))/2

同样的,我们还知道cos(a+b)=cosa*cosb-sina*sinb,cos(a-b)=cosa*cosb+sina*sinb

所以,把两式相加,我们就可以得到cos(a+b)+cos(a-b)=2cosa*cosb

所以我们就得到,cosa*cosb=(cos(a+b)+cos(a-b))/2

同理,两式相减我们就得到sina*sinb=-(cos(a+b)-cos(a-b))/2

这样,我们就得到了积化和差的四个公式:

sina*cosb=(sin(a+b)+sin(a-b))/2

cosa*sinb=(sin(a+b)-sin(a-b))/2

cosa*cosb=(cos(a+b)+cos(a-b))/2

sina*sinb=-(cos(a+b)-cos(a-b))/2

好,有了积化和差的四个公式以后,我们只需一个变形,就可以得到和差化积的四个公式.

我们把上述四个公式中的a+b设为x,a-b设为y,那么a=(x+y)/2,b=(x-y)/2

把a,b分别用x,y表示就可以得到和差化积的四个公式:

sinx+siny=2sin((x+y)/2)*cos((x-y)/2)

sinx-siny=2cos((x+y)/2)*sin((x-y)/2)

cosx+cosy=2cos((x+y)/2)*cos((x-y)/2)

cosx-cosy=-2sin((x+y)/2)*sin((x-y)/2)