1.圆的一般方程怎么解答？

2.已知两点，求圆的方程 例:已知A（1，-2），B（-3，6）则已AB为直径圆的方程是_____

3.圆的一般方程半径公式

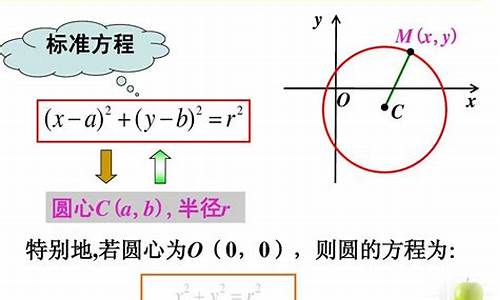
高考数学圆的方程_高中数学圆的方程题型

圆的几种方程:圆心-半径型:

(x-a)?十(y-b)?=r?

其中(x，y)是圆上任意点，(a，b)是圆心坐标，r是圆半径。

一般方程:

x?十y?十Cx十Dy十E=0

C，D，E是常数。

特点:平方项系数相等，不为零，没有xy项。

圆的一般方程怎么解答？

高二数学圆的方程如下：

x^2 +y^2=1

这就是一个二元二次函数，实际上表示的是一个圆形的方程，其圆心为(0,0)，而半径r=1，(x-a)?+(y-b)?=r? 都是圆形。

几何性质

圆的标准方程是(x-a)?+(y-b)?=r?，三个参数a、b、r，即圆心坐标为(a，b)，只要求出a、b、r，这时圆的方程就被确定，因此确定圆方程，须三个独立条件，其中圆心坐标是圆的定位条件，半径是圆的定形条件。 ?

圆的一般方程为 x^2+y^2+Dx+Ey+F=0 (D^2+E^2-4F>0)，（X+D/2）^2+（Y+E/2）^2=(D^2+E^2-4F)/4。圆的半径为 √[(D^2+E^2-4F)]/2即二分之一倍的根号下D的二次方加E的二次方减四倍的F。圆心坐标为 （-D/2，-E/2）。

特殊方程：x^2+y^2=1,圆心为（0，0）；半径为1

另外还有

标准方程：（x-a）^2+(y-b)^2=c^2,圆心为(a,b)；半径为c

一般方程：x^2+y^2+Dx+Ey+F=0(其中D^2+E^2-4F＞0）

已知两点，求圆的方程 例:已知A（1，-2），B（-3，6）则已AB为直径圆的方程是_____

圆的一般方程为 x?+y?+Dx+Ey+F=0 (D?+E?-4F>0)，或可以表示为(X+D/2)?+(Y+E/2)?=(D?+E?-4F)/4。其中圆心坐标是：（-D/2，-E/2）。半径：1/2√（D?+E?-4F）。

得出结论需知：

1、当D+E-4F=0时，一般方程仅表示一个点（-D/2，-E/2），叫做点圆(半径为零的圆)。

2、当D+E-4F<0肘，没有一个点的坐标满足圆的一般方程，即一般方程不表示任何图形，叫做虚圆。

圆的标准方程的优点在于它明确地指出了圆心和半径，而一般方程突出了方程式上的特点，便于区分曲线的形状。

圆的一般方程简介：

圆的一般方程，是数学领域的知识。圆是最常见的、最简单的一种二次曲线。圆的一般方程为 x2+y2+Dx+Ey+F=0 (D2+E2-4F>0)，或可以表示为(X+D/2)2+(Y+E/2)2=(D2+E2-4F)/4。

圆是最常见的、最简单的一种二次曲线。在平面上到一定点(中心)有同一距离(半径)之点的轨迹叫做圆周，简称圆。

圆的一般方程半径公式

解法如下：

|AB|=√［（－2-6)?+(-5-1)?]=10。

所以可得半径为5。

圆心坐标为：［（－2+6)/2,(-5+1)/2]=(2,-2)。

因此可得圆的方程为：（x-2)?+(y+2)?=5?。

圆的一般方程，是数学领域的知识。圆的一般方程为x2+y2+Dx+Ey+F=0 (D2+E2-4F>0)，或可以表示为（X+D/2)2+(Y+E/2)2=(D2+E2-4F)/4。

圆

是一种几何图形。根据定义，通常用圆规来画圆。 同圆内圆的直径、半径的长度永远相同，圆有无数条半径和无数条直径。圆是轴对称、中心对称图形。对称轴是直径所在的直线。 同时，圆又是“正无限多边形”，而“无限”只是一个概念。圆可以看成由无数个无限小的点组成的正多边形，当多边形的边数越多时，其形状、周长、面积就都越接近于圆。

圆的一般方程半径公式是r=1/2√（D?+E?-4F），圆的一般方程，是数学领域的知识，圆的一般方程为x2+y2+Dx+Ey+F=0（D2+E2-4F>0）。

圆是最常见的、最简单的一种二次曲线。在平面上到一定点有同一距离之点的轨迹叫做圆周，简称圆。圆半径的长度定出圆周的大小，圆心的位置确定圆在平面上的位置。圆的标准方程是一个关于x和y的二次方程。