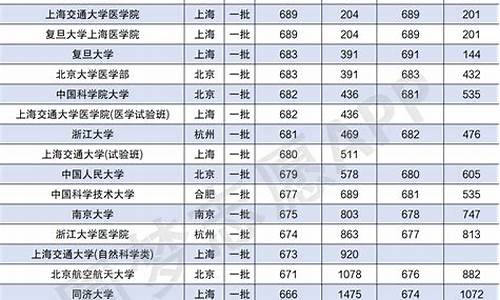
昨天高考数学_昨天高考数学题难吗

1.高考数学题

仅供参考（源于山东高考信息网）　 高考数学卷出现大量空白 过百就算不错的分数

6月15日，山东省高考正式阅卷进入第二天，阅卷速度明显比第一天快了。记者在山东大学的数学阅卷点得知，有些大题的阅卷进度非常快，已经阅卷过半。不过，今年不管是文科数学还是理科数学，第二卷普遍得分很低，有的大题在已阅完的23万份试卷中，有5万考生得到0分得满分的考生仅有80余人。

数学卷出现大量空白

往年高考，数学都是最令考生头疼的科目，今年也是如此，7日下午记者在考点采访时就发现，很多考生因为考题太难出考场时流露出失落的表情，很多平时数学成绩不错的考生也都喊题难。15日下午，记者在山东大学高考数学阅卷点采访的结果也印证了考生们的感受。

“今年数学确实有难度，我阅的那个题空白卷很多。”15日下午5时许，两位阅卷老师走出阅卷点后，开始交流起来。据这名老师介绍，他评阅的是理科数学的第21题，这道题是一道解析几何题，总分是13分，分为三道小题。这道题的得分非常不理想，最近两天，评阅这道题的老师一共阅了23万份试卷，结果很多考生的试卷都出现了空白，即便有些蒙上答案的，也没做对，有5万考生在这道题上得了0分，大部分考生只得了2分，即第一小题求抛物线方程算了出来，“得满分的也有，寥寥无几，大致数了数有80多个人吧。”

而文科数学的成绩情况也不容乐观。一位评阅文科数学最后一道题的老师表示，这道题很少有考生能得到满分，大部分考生的分数集中在3分、5分，即前两道小题答上了。其余题目也少见全部得满分的情况，大部分题目的分数在六七分左右。

部分题目已阅卷过半

由于很多大题出现大量空白卷，再加上已经过一天的训练，阅卷老师的阅卷速度加快了不少。“今天阅了3000多份，比昨天的速度快了近一倍。”一位批阅文科数学第17题的老师说，他的速度只能算是中游水平，有的老师一天能阅5000多份，这两天来，这道题已经阅了20多万份，接近总数的一半了，所以为了保持进度，当天下午他们还特意稍稍放慢了一点阅卷速度。

而记者了解到，像数学的填空题，只是看一下得数是不是正确，非常好阅，所以阅卷的进度非常快，阅完的试卷已经超过阅卷总数的一半，不少老师因此被调离这道题，改阅其他题目。

“照这个速度，再有两天就能全部阅完了，不过阅卷点有时间规定，也不能太早。”一位阅卷老师告诉记者，为了降低速度，有的题目下午阅卷时间还专门推迟了半个小时。

数学一道题5万人吃鸭蛋

有考生曾经向记者抱怨说，今年高考数学试题有些难，昨天参与数学阅卷的老师印证了考生的感觉。有阅卷老师表示，理科数学21题，也就是倒数第二道题，有很多考生吃了“鸭蛋”，而这样的试卷目前已经出现了5万多份。

一名理科数学的阅卷老师表示，21题是一道13分的题目，得满分的考生寥寥无几，从目前批阅的几十万份试卷看，满分考生只有八九十人，多数考生得分很低，仅仅有2分，更多的考生得了零分。19题则比较简单，平均得分超过了10分，而12分的满分考生很多。另外，文科数学的17题考生得分普遍比较高。

走出阅卷点，有阅卷老师初步分析，今年高考数学不管文科还是理科，想拿到满分很难，能在120分上下就算是高分了。有阅卷老师表示，高考数学阅卷速度相对比较快，阅卷量接近半数

文理科数学分都不高

“其实阅卷标准还是比较宽松的，但是数学阅卷不像作文，即使写得再多，如果没有得分点也不能给分 。”一位从事多年数学教学的阅卷老师告诉记者，他平时是教理科数学的，但这次被安排阅文科数学，所以在批阅文科数学的同时，他也非常关注理科数学的阅卷情况。

高考数学题

高考第一天考的语文和数学科目。

高考第一天考语文和数学两门科目。上午语文考试时间为9:00-11:30，下午数学考试时间为15:00-17:00。高考是限时考试，既考答题的准确度，又考答题的速度，要求既快又准确。一份试卷中各题的占分比例不一样。

高考科目设置：

高考科目设置通常包括语文、数学、英语、物理、化学、生物、政治、历史、地理等九个科目，其中语文和数学是必考科目。

考试难度：

1、语文考试，语文考试通常包括阅读理解、作文、短文改错、完形填空等多个部分。在备考时，考生需要注重积累常用词汇及句型，多读名著，提高阅读能力，还要注意写作技巧及规范性。

2、数学考试，数学考试包括数学基础知识应用、计算题和证明题等多个部分。在备考时，考生需要掌握数学基本公式，熟练运用各种计算方法，注意分析问题和解题思路，切忌粗心大意。

高考备考方法：

1、制订计划

在备考时，考生可以制订详细的复习计划，合理分配时间，并通过练习题和模拟考试来检验学习效果。

2、打牢基础

语文和数学是高考的必考科目，因此考生要重点复习语文基础知识和数学基本公式，这对后面的高考科目也有很大的帮助。

3、做练习题

做高考模拟试卷和历年高考真题对于备考非常有帮助，可以让考生熟悉考题类型，掌握解题技巧，提高答题速度和准确性。

4、心态调整

备考过程中，考生要保持积极乐观的心态，克服紧张情绪。同时注意休息，多进行体育锻炼，有助于身心健康，更好地应对考试。高考对于每个学生来说都是非常重要的，因此备考时要认真对待、有计划地复习。同时，在考试时保持冷静、认真答题，相信自己可以取得好成绩。

解：

1.

f'(x)=1-1/(1+x)------注意：这是导数;

所以：x>0时，原函数恒增;

又因为f(0)=0;

所以f(x)>0 在x>0时恒成立;

另：

1>a1>0;

所以：a2=f(a1)>0;

a3=f(a2)>0;

…… 易得：an=f(an-1)>0 n>=2 且n是整数 ;

（这里如果你觉得不稳妥的话可以用数学归纳法证明）;

另：

由题易得：an-a(n+1)=an-[an-ln(1+an)]=ln(1+an);

所以，只需要解出ln(1+an)>0即可得出：an>a(n+1);

又因为：an>0 (已解出);

所以：ln(1+an)>0;

即：an-a(n+1) >0;

即：a(n＋1)<an<a1<1;

所以：0<a(n+1)<an<1。

2.

原式等价于：an-ln(1+an)<an＾2／2;

设：F(an)=(an^2)/2 -an+ln(1+an);

（注意：在这里需要把an当做是一个连续的大于零的自变量而非间隔的单值）

则 F'(an)=an-1+1/(1+an)=(1+an)-2+1/(1+an)----恒等变换;这是导数;

（这一步的目的是变换成对号函数，这样好求解）

另设：t=1+an;

则：F'(x)=t-2+1/t>=0;

所以：F(x)恒增

（注：这里要是觉得不稳妥的话可以去证明一下导数不恒等于0，其实这里很明显导数是0时仅仅是个驻点而已）;

又因为F(0)=0;

an>0（已证明）;

所以F(an)>0;

即：F(an)=(an^2)/2 -an+ln(1+an)>0;

即：an-ln(1+an)<an＾2／2;

所以原式成立。

3.咕... 这一问没看明白你打的题目~...~|||

若是：b(n+1)=1/[2(n+1)bn]

先容我想想...

（我的惯用思路是把an的通项公式解出来，再把不等式移项到同侧，化函数解...不过，这里有个排列数...这样解不容易。另外一个思路就是想办法放缩，找到合适的中间量就ok了。亦或是用三段论，这样有时非常之简单。我一般用的就是这仨思路，这一问容我想想，我还没见过带排列数的不等式求解来着。）

我们老班经常会用一个函数跟三段论相结合的方法

就是先比较初值再利用比例把后面的相邻项之间的比算出来；

然后就利用单调性解决掉喽。

我先试试吧，昨天死活没算出来。

先用我们老班那方法吧，应该方便：

n=2时，易得：b2>a2*2;

（这里直接比较就可以，移到同侧和零比就行）

由题易得：b(n+1)/bn =(n+1)/2

----------a(n+1)*(n+1)!/an*n! =(n+1)*[an-ln(1+an)]/an ;

另：

设：g(x)= -ln(1+an)+ an/2;

则：g'(x)= -1/(1+an)+ 1/2;

0<an<1;

易得：g'(x)<0,g(x)恒减;

又因为：g(0)=0;

所以：g(an)<0;

所以：[an-ln(1+an)]/an <1/2;

所以：a(n+1)/an =(n+1)*[an-ln(1+an)]/an<(n+1)/2;

所以：a(n+1)*(n+1)!/an*n!<b(n+1)/bn;

又因为：n>=2且b2>a2*2;

所以：an*n!<bn。

答：1.0<a(n+1)<an<1；2.an＋1＜an＾2／2；3.an*n!<bn。

题解过程见上。

啊~~~~~~~~~~~~~竟然这样就行...~|||

真疯了...~昨天我在网吧对着电脑一个小时就硬生生的没能做出来~~~泪奔啊~~~

怪不得老班成天说我...~|||

呵呵，好了，大功告成：）